Posted Updated Analysis / Functional Analysis

The Big Three Pt. 4 - The Open Mapping Theorem (F-Space)

The Open Mapping Theorem

We are finally going to prove the open mapping theorem in $F$-space. In this version, only metric and completeness are required. Therefore it contains the Banach space version naturally.

(Theorem 0) Suppose we have the following conditions:

  1. $X$ is a $F$-space,
  2. $Y$ is a topological space,
  3. $\Lambda: X \to Y$ is continuous and linear, and
  4. $\Lambda(X)$ is of the second category in $Y$.

Then $\Lambda$ is an open mapping.

Proof. Let $B$ be a neighborhood of $0$ in $X$. Let $d$ be an invariant metric on $X$ that is compatible with the $F$-topology of $X$. Define a sequence of balls by

where $r$ is picked in such a way that $B_0 \subset B$. To show that $\Lambda$ is an open mapping, we need to prove that there exists some neighborhood $W$ of $0$ in $Y$ such that

To do this however, we need an auxiliary set. In fact, we will show that there exists some $W$ such that

We need to prove the inclusions one by one.

The first inclusion requires BCT. Since $B_2 -B_2 \subset B_1$, and $Y$ is a topological space, we get

Since

according to BCT, at least one $k\Lambda(B_2)$ is of the second category in $Y$. But scalar multiplication $y\mapsto ky$ is a homeomorphism of $Y$ onto $Y$, we see $k\Lambda(B_2)$ is of the second category for all $k$, especially for $k=1$. Therefore $\overline{\Lambda(B_2)}$ has nonempty interior, which implies that there exists some open neighborhood $W$ of $0$ in $Y$ such that $W \subset \overline{\Lambda(B_1)}$. By replacing the index, it’s easy to see this holds for all $n$. That is, for $n \geq 1$, there exists some neighborhood $W_n$ of $0$ in $Y$ such that $W_n \subset \overline{\Lambda(B_n)}$.

The second inclusion requires the completeness of $X$. Fix $y_1 \in \overline{\Lambda(B_1)}$, we will show that $y_1 \in \Lambda(B)$. Pick $y_n$ inductively. Assume $y_n$ has been chosen in $\overline{\Lambda(B_n)}$. As stated before, there exists some neighborhood $W_{n+1}$ of $0$ in $Y$ such that $W_{n+1} \subset \overline{\Lambda(B_{n+1})}$. Hence

Therefore there exists some $x_n \in B_n$ such that

Put $y_{n+1}=y_n-\Lambda x_n$, we see $y_{n+1} \in W_{n+1} \subset \overline{\Lambda(B_{n+1})}$. Therefore we are able to pick $y_n$ naturally for all $n \geq 1$.

Since $d(x_n,0)<\frac{r}{2^n}$ for all $n \geq 0$, the sums $z_n=\sum_{k=1}^{n}x_k$ converges to some $z \in X$ since $X$ is a $F$-space. Notice we also have

we have $z \in B_0 \subset B$.

By the continuity of $\Lambda$, we see $\lim_{n \to \infty}y_n = 0$. Notice we also have

we see $y_1 = \Lambda z \in \Lambda(B)$.

The whole theorem is now proved, that is, $\Lambda$ is an open mapping. $\square$

Remarks

You may think the following relation comes from nowhere:

But it’s not. We need to review some set-point topology definitions. Notice that $y_n$ is a limit point of $\Lambda(B_n)$, and $y_n-W_{n+1}$ is a open neighborhood of $y_n$. If $(y_n - W_{n+1}) \cap \Lambda(B_{n})$ is empty, then $y_n$ cannot be a limit point.

The geometric series by

is widely used when sum is taken into account. It is a good idea to keep this technique in mind.

Corollaries

The formal proof will not be put down here, but they are quite easy to be done.

(Corollary 0) $\Lambda(X)=Y$.

This is an immediate consequence of the fact that $\Lambda$ is open. Since $Y$ is open, $\Lambda(X)$ is an open subspace of $Y$. But the only open subspace of $Y$ is $Y$ itself.

(Corollary 1) $Y$ is a $F$-space as well.

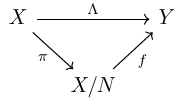
If you have already see the commutative diagram by quotient space (put $N=\ker\Lambda$), you know that the induced map $f$ is open and continuous. By treating topological spaces as groups, by corollary 0 and the first isomorphism theorem, we have

Therefore $f$ is a isomorphism; hence one-to-one. Therefore $f$ is a homeomorphism as well. In this post we showed that $X/\ker{\Lambda}$ is a $F$-space, therefore $Y$ has to be a $F$-space as well. (We are using the fact that $\ker{\Lambda}$ is a closed set. But why closed?)

(Corollary 2) If $\Lambda$ is a continuous linear mapping of an $F$-space $X$ onto a $F$-space $Y$, then $\Lambda$ is open.

This is a direct application of BCT and open mapping theorem. Notice that $Y$ is now of the second category.

(Corollary 3) If the linear map $\Lambda$ in Corollary 2 is injective, then $\Lambda^{-1}:Y \to X$ is continuous.

This comes from corollary 2 directly since $\Lambda$ is open.

(Corollary 4) If $X$ and $Y$ are Banach spaces, and if $\Lambda: X \to Y$ is a continuous linear bijective map, then there exist positive real numbers $a$ and $b$ such that

for every $x \in X$.

This comes from corollary 3 directly since both $\Lambda$ and $\Lambda^{-1}$ are bounded as they are continuous.

(Corollary 5) If $\tau_1 \subset \tau_2$ are vector topologies on a vector space $X$ and if both $(X,\tau_1)$ and $(X,\tau_2)$ are $F$-spaces, then $\tau_1 = \tau_2$.

This is obtained by applying corollary 3 to the identity mapping $\iota:(X,\tau_2) \to (X,\tau_1)$.

(Corollary 6) If $\lVert \cdot \rVert_1$ and $\lVert \cdot \rVert_2$ are two norms in a vector space $X$ such that

  • $\lVert\cdot\rVert_1 \leq K\lVert\cdot\rVert_2$.
  • $(X,\lVert\cdot\rVert_1)$ and $(X,\lVert\cdot\rVert_2)$ are Banach

Then $\lVert\cdot\rVert_1$ and $\lVert\cdot\rVert_2$ are equivalent.

This is merely a more restrictive version of corollary 5.

The series

Since there is no strong reason to write more posts on this topic, i.e. the three fundamental theorems of linear functional analysis, I think it’s time to make a list of the series. It’s been around half a year.

Posted Updated Analysis / Functional Analysis / Topological Vector Space

The completeness of the quotient space (topological vector space)

The Goal

We are going to show the completeness of $X/N$ where $X$ is a TVS and $N$ a closed subspace. Alongside, a bunch of useful analysis tricks will be demonstrated (and that’s why you may find this blog post a little tedious.). But what’s more important, the theorem proved here will be used in the future.

The main process

To make it clear, we should give a formal definition of $F$-space.

A topological space $X$ is an $F$-space if its topology $\tau$ is induced by a complete invariant metric $d$.

A metric $d$ on a vector space $X$ will be called invariant if for all $x,y,z \in X$, we have

By complete we mean every Cauchy sequence of $(X,d)$ converges.

Defining the quotient metric $\rho$

The metric can be inherited to the quotient space naturally (we will use this fact latter), that is

If $X$ is a $F$-space, $N$ is a closed subspace of a topological vector space $X$, then $X/N$ is still a $F$-space.

Suppose $d$ is a complete invariant metric compatible with $\tau_X$. The metric on $X/N$ is defined by

$\rho$ is a metric

Proof. First, if $\pi(x)=\pi(y)$, that is, $x-y \in N$, we see

If $\pi(x) \neq \pi(y)$ however, we shall show that $\rho(\pi(x),\pi(y))>0$. In this case, we have $x-y \notin N$. Since $N$ is closed, $N^c$ is open, and $x-y$ is an interior point of $X-N$. Therefore there exists an open ball $B_r(x-y)$ centered at $x-y$ with radius $r>0$ such that $B_r(x-y) \cap N = \varnothing$. Notice we have $d(x-y,z)>r$ since otherwise $z \in B_r(x-y)$. By putting

we see $d(x-y,z) \geq r_0$ for all $z \in N$ and indeed $r_0=\inf_{z \in N}d(x-y,z)>0$ (the verification can be done by contradiction). In general, $\inf_z d(x-y,z)=0$ if and only if $x-y \in \overline{N}$.

Next, we shall show that $\rho(\pi(x),\pi(y))=\rho(\pi(y),\pi(x))$, and it suffices to assume that $\pi(x) \neq \pi(y)$. Sgince $d$ is translate invariant, we get

Therefore the $\inf$ of the left hand is equal to the one of the right hand. The identity is proved.

Finally, we need to verify the triangle inequality. Let $r,s,t \in X$. For any $\varepsilon>0$, there exist some $z_\varepsilon$ and $z_\varepsilon’$ such that

Since $d$ is invariant, we see

(I owe @LeechLattice for the inequality above.)

Therefore

(Warning: This does not imply that $\rho(\pi(r),\pi(s))+\rho(\pi(s),\pi(t))=\inf_z d(r-t,z)$ since we don’t know whether it is the lower bound or not.)

If $\rho(\pi(r),\pi(s))+\rho(\pi(s),\pi(t))<\rho(\pi(r),\pi(t))$ however, let

then there exists some $z’’_\varepsilon=z_\varepsilon+z’_\varepsilon$ such that

which is a contradiction since $\rho(\pi(r),\pi(t)) \leq d(r-t,z)$ for all $z \in N$.

(We are using the $\varepsilon$ definition of $\inf$. See here.)

$\rho$ is translate invariant

Since $\pi$ is surjective, we see if $u \in X/N$, there exists some $a \in X$ such that $\pi(a)=u$. Therefore

$\rho$ is well-defined

If $\pi(x)=\pi(x’)$ and $\pi(y)=\pi(y’)$, we have to show that $\rho(\pi(x),\pi(y))=\rho(\pi(x’),\pi(y’))$. In fact,

since $\rho(\pi(x),\pi(x’))=0$ as $\pi(x)=\pi(x’)$. Meanwhile

therefore $\rho(\pi(x),\pi(y))=\rho(\pi(x’),\pi(y’))$.

$\rho$ is compatible with $\tau_N$

By proving this, we need to show that a set $E \subset X/N$ is open with respect to $\tau_N$ if and only if $E$ is a union of open balls. But we need to show a generalized version:

If $\mathscr{B}$ is a local base for $\tau$, then the collection $\mathscr{B}_N$, which contains all sets $\pi(V)$ where $V \in \mathscr{B}$, forms a local base for $\tau_N$.

Proof. We already know that $\pi$ is continuous, linear and open. Therefore $\pi(V)$ is open for all $V \in \mathscr{B}$. For any open set around $E \subset X/N$ containing $\pi(0)$, we see $\pi^{-1}(E)$ is open, and we have

and therefore

Now consider the local base $\mathscr{B}$ containing all open balls around $0 \in X$. Since

we see $\rho$ determines $\mathscr{B}_N$. But we have already proved that $\rho$ is invariant; hence $\mathscr{B}_N$ determines $\tau_N$.

If $d$ is complete, then $\rho$ is complete.

Once this is proved, we are able to claim that, if $X$ is a $F$-space, then $X/N$ is still a $F$-space, since its topology is induced by a complete invariant metric $\rho$.

Proof. Suppose $(x_n)$ is a Cauchy sequence in $X/N$, relative to $\rho$. There is a subsequence $(x_{n_k})$ with $\rho(x_{n_k},x_{n_{k+1}})<2^{-k}$. Since $\pi$ is surjective, we are able to pick some $z_k \in X$ such that $\pi(z_k) = x_{n_k}$ and such that

(The existence can be verified by contradiction still.) By the inequality above, we see $(z_k)$ is Cauchy (can you see why?). Since $X$ is complete, $z_k \to z$ for some $z \in X$. By the continuity of $\pi$, we also see $x_{n_k} \to \pi(z)$ as $k \to \infty$. Therefore $(x_{n_k})$ converges. Hence $(x_n)$ converges since it has a convergent subsequence. $\rho$ is complete.

Remarks

This fact will be used to prove some corollaries in the open mapping theorem. For instance, for any continuous linear map $\Lambda:X \to Y$, we see $\ker(\Lambda)$ is closed, therefore if $X$ is a $F$-space, then $X/\ker(\Lambda)$ is a $F$-space as well. We will show in the future that $X/\ker(\Lambda)$ and $\Lambda(X)$ are homeomorphic if $\Lambda(X)$ is of the second category.

There are more properties that can be inherited by $X/N$ from $X$. For example, normability, metrizability, local convexity. In particular, if $X$ is Banach, then $X/N$ is Banach as well. To do this, it suffices to define the quotient norm by

Posted Updated Analysis / Elementary / Continuity

Basic Facts of Semicontinuous Functions

Continuity

We are restricting ourselves into $\mathbb{R}$ endowed with normal topology. Recall that a function is continuous if and only if for any open set $U \subset \mathbb{R}$, we have

to be open. One can rewrite this statement using $\varepsilon-\delta$ language. To say a function $f: \mathbb{R} \to \mathbb{R}$ continuous at $f(x)$, we mean for any $\varepsilon>0$, there exists some $\delta>0$ such that for $t \in (x-\delta,x+\delta)$, we have

$f$ is continuous on $\mathbb{R}$ if and only if $f$ is continuous at every point of $\mathbb{R}$.

If $(x-\delta,x+\delta)$ is replaced with $(x-\delta,x)$ or $(x,x+\delta)$, we get left continuous and right continuous, one of which plays an important role in probability theory.

But the problem is, sometimes continuity is too strong for being a restriction, but the ‘direction’ associated with left/right continuous functions are unnecessary as well. For example the function

is neither left nor right continuous (globally), but it is a thing. Left/right continuity is not a perfectly weakened version of continuity. We need something different.

Definition of semicontinuous

Let $f$ be a real (or extended-real) function on $\mathbb{R}$. The semicontinuity of $f$ is defined as follows.

If

is open for all real $\alpha$, we say $f$ is lower semicontinuous.

If

is open for all real $\alpha$, we say $f$ is upper semicontinuous.

Is it possible to rewrite these definitions à la $\varepsilon-\delta$? The answer is yes if we restrict ourselves in metric space.

$f: \mathbb{R} \to \mathbb{R}$ is upper semicontinuous at $x$ if, for every $\varepsilon>0$, there exists some $\delta>0$ such that for $t \in (x-\delta,x+\delta)$, we have

$f: \mathbb{R} \to \mathbb{R}$ is lower semicontinuous at $x$ if, for every $\varepsilon>0$, there exists some $\delta>0$ such that for $t \in (x-\delta,x+\delta)$, we have

Of course, $f$ is upper/lower semicontinuous on $\mathbb{R}$ if and only if it is so on every point of $\mathbb{R}$. One shall find no difference between the definitions in different styles.

Relation with continuous functions

Here is another way to see it. For the continuity of $f$, we are looking for arbitrary open subsets $V$ of $\mathbb{R}$, and $f^{-1}(V)$ is expected to be open. For the lower/upper semicontinuity of $f$, however, the open sets are restricted to be like $(\alpha,+\infty]$ and $[-\infty,\alpha)$. Since all open sets of $\mathbb{R}$ can be generated by the union or intersection of sets like $[-\infty,\alpha)$ and $(\beta,+\infty]$, we immediately get

$f$ is continuous if and only if $f$ is both upper semicontinuous and lower semicontinuous.

Proof. If $f$ is continuous, then for any $\alpha \in \mathbb{R}$, we see $[-\infty,\alpha)$ is open, and therefore

has to be open. The upper semicontinuity is proved. The lower semicontinuity of $f$ is proved in the same manner.

If $f$ is both upper and lower semicontinuous, we see

is open. Since every open subset of $\mathbb{R}$ can be written as a countable union of segments of the above types, we see for any open subset $V$ of $\mathbb{R}$, $f^{-1}(V)$ is open. (If you have trouble with this part, it is recommended to review the definition of topology.) $\square$

Examples

There are two important examples.

  1. If $E \subset \mathbb{R}$ is open, then $\chi_E$ is lower semicontinuous.
  2. If $F \subset \mathbb{R}$ is closed, then $\chi_F$ is upper semicontinuous.

We will prove the first one. The second one follows in the same manner of course. For $\alpha<0$, the set $A=\chi_E^{-1}((\alpha,+\infty])$ is equal to $\mathbb{R}$, which is open. For $\alpha \geq 1$, since $\chi_E \leq 1$, we see $A=\varnothing$. For $0 \leq \alpha < 1$ however, the set of $x$ where $\chi_E>\alpha$ has to be $E$, which is still open.

When checking the semicontinuity of a function, we check from bottom to top or top to bottom. The function $\chi_E$ is defined by

Addition of semicontinuous functions

If $f_1$ and $f_2$ are upper/lower semicontinuous, then so is $f_1+f_2$.

Proof. We are going to prove this using different tools. Suppose now both $f_1$ and $f_2$ are upper semicontinuous. For $\varepsilon>0$, there exists some $\delta_1>0$ and $\delta_2>0$ such that

Proof. If we pick $\delta=\min(\delta_1,\delta_2)$, then we see for all $t \in (x-\delta,x+\delta)$, we have

The upper semicontinuity of $f_1+f_2$ is proved by considering all $x \in \mathbb{R}$.

Now suppose both $f_1$ and $f_2$ are lower semicontinuous. We have an identity by

The set on the right side is always open. Hence $f_1+f_2$ is lower semicontinuous. $\square$

However, when there are infinite many semicontinuous functions, things are different.

Let $\{f_n\}$ be a sequence of nonnegative functions on $\mathbb{R}$, then

  • If each $f_n$ is lower semicontinuous, then so is $\sum_{1}^{\infty}f_n$.
  • If each $f_n$ is upper semicontinuous, then $\sum_{1}^{\infty}f_n$ is not necessarily upper semicontinuous.

Proof. To prove this we are still using the properties of open sets. Put $g_n=\sum_{1}^{n}f_k$. Now suppose all $f_k$ are lower. Since $g_n$ is a finite sum of lower functions, we see each $g_n$ is lower. Let $f=\sum_{n}f_n$. As $f_k$ are non-negative, we see $f(x)>\alpha$ if and only if there exists some $n_0$ such that $g_{n_0}(x)>\alpha$. Therefore

The set on the right hand is open already.

For the upper semicontinuity, it suffices to give a counterexample, but before that, we shall give the motivation.

As said, the characteristic function of a closed set is upper semicontinuous. Suppose $\{E_n\}$ is a sequence of almost disjoint closed set, then $E=\cup_{n\geq 1}E_n$ is not necessarily closed, therefore $\chi_E=\sum\chi_{E_n}$ (a.e.) is not necessarily upper semicontinuous. Now we give a concrete example. Put $f_0=\chi_{[1,+\infty]}$ and $f_n=\chi_{E_n}$ for $n \geq 1$ where

For $x > 0$, we have $f=\sum_nf_n \geq 1$. Meanwhile, $f^{-1}([-\infty,1))=[-\infty,0]$, which is not open. $\square$

Notice that $f$ can be defined on any topological space here.

Maximum and minimum

There is one fact we already know about continuous functions.

If $X$ is compact, $f: X \to \mathbb{R}$ is continuous, then there exists some $a,b \in X$ such that $f(a)=\min f(X)$, $f(b)=\max f(X)$.

In fact, $f(X)$ is compact still. But for semicontinuous functions, things will be different but reasonable. For upper semicontinuous functions, we have the following fact.

If $X$ is compact and $f: X \to (-\infty,+\infty)$ is upper semicontinuous, then there exists some $a \in X$ such that $f(a)=\max f(X)$.

Notice that $X$ is not assumed to hold any other topological property. It can be Hausdorff or Lindelöf, but we are not asking for restrictions like this. The only property we will be using is that every open cover of $X$ has a finite subcover. Of course, one can replace $X$ with any compact subset of $\mathbb{R}$, for example, $[a,b]$.

Proof. Put $\alpha=\sup f(X)$, and define

If $f$ attains no maximum, then for any $x \in X$, there exists some $n \geq 1$ such that $f(x)<\alpha-\frac{1}{n}$. That is, $x \in E_n$ for some $n$. Therefore $\bigcup_{n \geq 1}E_n$ covers $X$. But this cover has no finite subcover of $X$. A contradiction since $X$ is compact. $\square$

Approximating integrable functions

This is a comprehensive application of several properties of semicontinuity.

(Vitali–Carathéodory theorem) Suppose $f \in L^1(\mathbb{R})$, where $f$ is a real-valued function. For $\varepsilon>0$, there exist some functions $u$ and $v$ on $\mathbb{R}$ such that $u \leq f \leq v$, $u$ is an upper semicontinuous function bounded above, and $v$ is lower semicontinuous bounded below, and

It suffices to prove this theorem for $f \geq 0$ (of course $f$ is not identically equal to $0$ since this case is trivial). Since $f$ is the pointwise limit of an increasing sequence of simple functions $s_n$, can to write $f$ as

By putting $t_1=s_1$, $t_n=s_n-s_{n-1}$ for $n \geq 2$, we get $f=\sum_n t_n$. We can write $f$ as

where $E_k$ is measurable for all $k$. Also, we have

and the series on the right hand converges (since $f \in L^1$. By the properties of Lebesgue measure, there exists a compact set $F_k$ and an open set $V_k$ such that $F_k \subset E_k \subset V_k$ and $c_km(V_k-F_k)<\frac{\varepsilon}{2^{k+1}}$. Put

(now you can see $v$ is lower semicontinuous and $u$ is upper semicontinuous). The $N$ is chosen in such a way that

Since $V_k \supset E_k$, we have $\chi_{V_k} \geq \chi_{E_k}$. Therefore $v \geq f$. Similarly, $f \geq u$. Now we need to check the desired integral inequality. A simple recombination shows that

If we integrate the function above, we get

This proved the case when $f \geq 0$. In the general case, we write $f=f^{+}-f^{-}$. Attach the semicontinuous functions to $f^{+}$ and $f^{-}$ respectively by $u_1 \leq f^{+} \leq v_1$ and $u_2 \leq f^{-} \leq v_2$. Put $u=u_1-v_2$, $v=v_1-u_2$. As we can see, $u$ is upper semicontinuous and $v$ is lower semicontinuous. Also, $u \leq f \leq v$ with the desired property since

and the theorem follows. $\square$

Generalisation

Indeed, the only property about measure used is the existence of $F_k$ and $V_k$. The domain $\mathbb{R}$ here can be replaced with $\mathbb{R}^k$ for $1 \leq k < \infty$, and $m$ be replaced with the respective $m_k$. Much more generally, the domain can be replaced by any locally compact Hausdorff space $X$ and the measure by any measure associated with the Riesz-Markov-Kakutani representation theorem on $C_c(X)$.

Is the reverse approximation always possible?

The answer is no. Consider the fat Cantor set $K$, which has Lebesgue measure $\frac{1}{2}$. We shall show that $\chi_K$ can not be approximated below by a lower semicontinuous function.

If $v$ is a lower semicontinuous function such that $v \leq \chi_K$, then $v \leq 0$.

Proof. Consider the set $V=v^{-1}((0,1])=v^{-1}((0,+\infty))$. Since $v \leq \chi_K$, we have $V \subset K$. We will show that $V$ has to be empty.

Pick $t \in V$. Since $V$ is open, there exists some neighbourhood $U$ containing $t$ such that $U \subset V$. But $U=\varnothing$ since $U \subset K$ and $K$ has an empty interior. Therefore $V = \varnothing$. That is, $v \leq 0$ for all $x$. $\square$

Suppose $u$ is an upper semicontinuous function such that $u \geq f$. For $\varepsilon=\frac{1}{2}$, we have

This example shows that there exist some integrable functions that are not able to reversely approximated in the sense of the Vitali–Carathéodory theorem.

Posted Updated Analysis / Functional Analysis / Topological Vector Space

An Introduction to Quotient Space

I’m assuming the reader has some abstract algebra and functional analysis background. You may have learned this already in your linear algebra class, but we are making our way to functional analysis problems.

Motivation

The trouble with $L^p$ spaces

Fix $p$ with $1 \leq p \leq \infty$. It’s easy to see that $L^p(\mu)$ is a topological vector space. But it is not a metric space if we define

The reason is, if $d(f,g)=0$, we can only get $f=g$ a.e., but they are not strictly equal. With that being said, this function $d$ is actually a pseudo metric. This is unnatural. However, the relation $\sim$ by $f \sim g \mathbb{R}ightarrow d(f,g)=0$ is a equivalence relation. This inspires us to take the quotient set into consideration.

Vector spaces are groups anyway

For a vector space $V$, every subspace of $V$ is a normal subgroup. There is no reason to prevent ourselves from considering the quotient group and looking for some interesting properties. Further, a vector space is an abelian group, therefore any subspace is automatically normal.

Definition

Let $N$ be a subspace of a vector space $X$. For every $x \in X$, let $\pi(x)$ be the coset of $N$ that contains $x$, that is

Trivially, $\pi(x)=\pi(y)$ if and only if $x-y \in N$ (say, $\pi$ is well-defined since $N$ is a vector space). This is a linear function since we also have the addition and multiplication by

These cosets are the elements of a vector space $X/N$, which reads, the quotient space of $X$ modulo $N$. The map $\pi$ is called the canonical map as we all know.

Examples

R^2-quotient

First, we shall treat $\mathbb{R}^2$ as a vector space, and the subspace $\mathbb{R}$, which is graphically represented by $x$-axis, as a subspace (we will write it as $X$). For a vector $v=(2,3)$, which is represented by $AB$, we see the coset $v+X$ has something special. Pick any $u \in X$, for example, $AE$, $AC$, or $AG$. We see $v+u$ has the same $y$ value. The reason is simple since we have $v+u=(2+x,3)$, where the $y$ value remains fixed however $u$ may vary.

With that being said, the set $v+X$, which is not a vector space, can be represented by $\overrightarrow{AD}$. This proceed can be generalized to $\mathbb{R}^n$ with $\mathbb{R}^m$ as a subspace with ease.

We now consider a fancy example. Consider all rational Cauchy sequences, that is

where $a_k\in\mathbb{Q}$ for all $k$. In analysis class, we learned two facts.

  1. Any Cauchy sequence is bounded.
  2. If $(a_n)$ converges, then $(a_n)$ is Cauchy.

However, the reverse of 2 does not hold in $\mathbb{Q}$. For example, if we put $a_k=(1+\frac{1}{k})^k$, we should have the limit to be $e$, but $e \notin \mathbb{Q}$.

If we define the addition and multiplication term by term, namely

and

where $\alpha \in \mathbb{Q}$, we get a vector space (the verification is easy). The zero vector is defined by

This vector space is denoted by $\overline{\mathbb{Q}}$. The subspace containing all sequences converges to $0$ will be denoted by $\overline{\mathbb{O}}$. Again, $(a_n)+\overline{\mathbb{O}}=(b_n)+\overline{\mathbb{O}}$ if and only if $(a_n-b_n) \in \overline{\mathbb{O}}$. Using the language of equivalence relation, we also say $(a_n)$ and $(b_n)$ are equivalent if $(a_n-b_n) \in \overline{\mathbb{O}}$. For example, the two following sequences are equivalent:

Actually, we will get $\mathbb{R} \simeq \overline{\mathbb{Q}}/\overline{\mathbb{O}}$ in the end. But to make sure that this quotient space is exactly the one we meet in our analysis class, there are a lot of verifications should be done.

We shall give more definitions for calculation. The multiplication of two Cauchy sequences is defined term by term à la the addition. For $\overline{\mathbb{Q}}/\overline{\mathbb{O}}$ we have

and

As for inequality, a partial order has to be defined. We say $(a_n) > (0)$ if there exists some $N>0$ such that $a_n>0$ for all $n \geq N$. By $(a_n) > (b_n)$ we mean $(a_n-b_n)>(0)$ of course. For cosets, we say $(a_n)+\overline{\mathbb{O}}>\overline{\mathbb{O}}$ if $(x_n) > (0)$ for some $(x_n) \in (a_n)+\overline{\mathbb{O}}$. This is well defined. That is, if $(x_n)>(0)$, then $(y_n)>(0)$ for all $(y_n) \in (a_n)+\overline{\mathbb{O}}$.

With these operations being defined, it can be verified that $\overline{\mathbb{Q}}/\overline{\mathbb{O}}$ has the desired properties, for example, the least-upper-bound property. But this goes too far from the topic, we are not proving it here. If you are interested, you may visit here for more details.

Finally, we are trying to make $L^p$ a Banach space. Fix $p$ with $1 \leq p < \infty$. There is a seminorm defined for all Lebesgue measurable functions on $[0,1]$ by

$L^p$ is a vector space containing all functions $f$ with $p(f)<\infty$. But it’s not a normed space by $p$, since $p(f)=0$ only implies $f=0$ almost everywhere. However, the set $N$ which contains all functions that equal $0$ is also a vector space. Now consider the quotient space by

where $\pi$ is the canonical map of $L^p$ into $L^p/N$. We shall prove that $\tilde{p}$ is well-defined here. If $\pi(f)=\pi(g)$, we have $f-g \in N$, therefore

which forces $p(f)=p(g)$. Therefore in this case we also have $\tilde{p}(\pi(f))=\tilde{p}(\pi(g))$. This indeed ensures that $\tilde{p}$ is a norm, and $L^p/N$ a Banach space. There are some topological facts required to prove this, we are going to cover a few of them.

Topology of quotient space

Definition

We know if $X$ is a topological vector space with a topology $\tau$, then the addition and scalar multiplication are continuous. Suppose now $N$ is a closed subspace of $X$. Define $\tau_N$ by

We are expecting $\tau_N$ to be properly-defined. And fortunately, it is. Some interesting techniques will be used in the following section.

$\tau_N$ is a vector topology

There will be two steps to get this done.

$\tau_N$ is a topology.

It is trivial that $\varnothing$ and $X/N$ are elements of $\tau_N$. Other properties are immediate as well since we have

and

That said, if we have $A,B\in \tau_N$, then $A \cap B \in \tau_N$ since $\pi^{-1}(A \cap B)=\pi^{-1}(A) \cap \pi^{-1}(B) \in \tau$.

Similarly, if $A_\alpha \in \tau_N$ for all $\alpha$, we have $\cup A_\alpha \in \tau_N$. Also, by definition of $\tau_N$, $\pi$ is continuous.

$\tau_N$ is a vector topology.

First, we show that a point in $X/N$, which can be written as $\pi(x)$, is closed. Notice that $N$ is assumed to be closed, and

therefore has to be closed.

In fact, $F \subset X/N$ is $\tau_N$-closed if and only if $\pi^{-1}(F)$ is $\tau$-closed. To prove this, one needs to notice that $\pi^{-1}(F^c)=(\pi^{-1}(F))^{c}$.

Suppose $V$ is open, then

is open. By definition of $\tau_N$, we have $\pi(V) \in \tau_N$. Therefore $\pi$ is an open mapping.

If now $W$ is a neighbourhood of $0$ in $X/N$, there exists a neighbourhood $V$ of $0$ in $X$ such that

Hence $\pi(V)+\pi(V) \subset W$. Since $\pi$ is open, $\pi(V)$ is a neighbourhood of $0$ in $X/N$, this shows that the addition is continuous.

The continuity of scalar multiplication will be shown in a direct way (so can the addition, but the proof above is intended to offer some special technique). We already know, the scalar multiplication on $X$ by

is continuous, where $\Phi$ is the scalar field (usually $\mathbb{R}$ or $\mathbb{C}$. Now the scalar multiplication on $X/N$ is by

We see $\psi(\alpha,x+N)=\pi(\varphi(\alpha,x))$. But the composition of two continuous functions is continuous, therefore $\psi$ is continuous.

A commutative diagram by quotient space

We are going to talk about a classic commutative diagram that you already see in algebra class.

diagram-000001

There are some assumptions.

  1. $X$ and $Y$ are topological vector spaces.
  2. $\Lambda$ is linear.
  3. $\pi$ is the canonical map.
  4. $N$ is a closed subspace of $X$ and $N \subset \ker\Lambda$.

Algebraically, there exists a unique map $f: X/N \to Y$ by $x+N \mapsto \Lambda(x)$. Namely, the diagram above is commutative. But now we are interested in some analysis facts.

$f$ is linear.

This is obvious. Since $\pi$ is surjective, for $u,v \in X/N$, we are able to find some $x,y \in X$ such that $\pi(x)=u$ and $\pi(y)=v$. Therefore we have

and

$\Lambda$ is open if and only if $f$ is open.

If $f$ is open, then for any open set $U \subset X$, we have

to be an open set since $\pi$ is open, and $\pi(U)$ is an open set.

If $f$ is not open, then there exists some $V \subset X/N$ such that $f(V)$ is closed. However, since $\pi$ is continuous, we have $\pi^{-1}(V)$ to be open. In this case, we have

to be closed. $\Lambda$ is therefore not open. This shows that if $\Lambda$ is open, then $f$ is open.

$\Lambda$ is continuous if and only if $f$ is continuous.

If $f$ is continuous, for any open set $W \subset Y$, we have $\pi^{-1}(f^{-1}(W))=\Lambda^{-1}(W)$ to be open. Therefore $\Lambda$ is continuous.

Conversely, if $\Lambda$ is continuous, for any open set $W \subset Y$, we have $\Lambda^{-1}(W)$ to be open. Therefore $f^{-1}(W)=\pi(\Lambda^{-1}(W))$ has to be open since $\pi$ is open.

Posted Updated Analysis / Functional Analysis

The Big Three Pt. 3 - The Open Mapping Theorem (Banach Space)

What is open mapping

An open map is a function between two topological spaces that maps open sets to open sets. Precisely speaking, a function $f: X \to Y$ is open if for any open set $U \subset X$, $f(U)$ is open in $Y$. Likewise, a closed map is a function mapping closed sets to closed sets.

You may think open/closed map is an alternative name of continuous function. But it’s not. The definition of open/closed mapping is totally different from continuity. Here are some simple examples.

  1. $f(x)=\sin{x}$ defined on $\mathbb{R}$ is not open, though it’s continuous. It can be verified by considering $(0,2\pi)$, since we have $f((0,2\pi))=[-1,1]$.
  2. The projection $\pi: \mathbb{R}^2 \to \mathbb{R}$ defined by $(x,y) \mapsto x$ is open. Indeed, it maps an open ball onto an open interval on $x$ axis.
  3. The inclusion map $\varphi: \mathbb{R} \to \mathbb{R}^2$ by $x \mapsto (x,0)$ however, is not open. An open interval on the plane is locally closed but not open or closed.

Under what condition will a continuous linear function between two TVS be an open mapping? We’ll give the answer in this blog post. Open mapping theorem is a sufficient condition on whether a continuous linear function is open.

Open Mapping Theorem

Let $X,Y$ be Banach spaces and $T: X \to Y$ a surjective bounded linear map. Then $T$ is an open mapping.

The open balls in $X$ and $Y$ are defined respectively by

All we need to do is show that there exists some $r>0$ such that

Since every open set in $X$ or $Y$ can be expressed as a union of open balls. For a ball in $X$ centered at $x \in X$ with radius $r$, we can express it as $x+B_r^X$. After that, it becomes obvious that $T$ maps open set to open set.

First we have

The surjectivity of $T$ ensures that

Since $Y$ is Banach, or simply a complete metric space, by Baire category theorem, there must be some $n_0 \in \mathbb{N}$ such that $\overline{T(B_{n_0}^{X})}$ has nonempty interior. If not, which means $T(B_n^{X})$ is nowhere dense for all $n \in \mathbb{N}$, we have $Y$ is of the first category. A contradiction.

Since $x \to nx$ is a homeomorphism of $X$ onto $X$, we see in fact $T(B_n^X)$ is not nowhere dense for all $n \in \mathbb{N}$. Therefore, there exists some $y_0 \in \overline{T(B_1^{X})}$ and some $\varepsilon>0$ such that

the open set on the left hand is a neighborhood of $y_0$, which should be in the interior of $\overline{T(B_1^X)}$.

On the other hand, we claim

We shall prove it as follows. Pick any $y \in \overline{T(B_1^X)}$, we shall show that $y-y_0 \in \overline{T(B_2^X)}$. For $y_0$, there exists a sequence of $y_n$ where $\lVert y_n \rVert <1$ for all $n$ such that $Ty_n \to y_0$. Also we are able to find a sequence of $x_n$ where $\lVert x_n \rVert <1$ for all $n$ such that $Tx_n \to y$. Notice that we also have

since

we see $T(x_n-y_n) \in T(B_2^X)$ for all $n$, it follows that

Combining all these relations, we get

Since $T$ is linear, we see

By induction we get

for all $n \geq 1$.

We shall show however

For any $u \in B_{\varepsilon/4}^Y$, we have $u \in \overline{T(B_{1/2}^X)}$. There exists some $x_1 \in B_{1/2}^{X}$ such that

This implies that $u-Tx_1 \in B_{\varepsilon/8}^Y$. Under the same fashion, we are able to pick $x_n$ in such a way that

where $\lVert x_n \rVert<2^{-n}$. Now let $z_n=\sum_{k=1}^{n}x_k$, we shall show that $(z_n)$ is Cauchy. For $m<n$, we have

Since $X$ is Banach, there exists some $z \in X$ such that $z_n \to z$. Further we have

therefore $z \in B_1^X$. Since $T$ is bounded, therefore continuous, we get $T(z)=u$. To summarize, for $u \in B_{\varepsilon/4}^Y$, we have some $z \in B_{1}^X$ such that $T(z)=y$, which implies $T(B_1^X) \supset B_{\varepsilon/4}^Y$.

Let $U \subset X$ be open, we want to show that $T(U)$ is also open. Take $y \in T(U)$, then $y=T(x)$ with $x \in U$. Since $U$ is open, there exists some $\varepsilon>0$ such that $B_{\varepsilon}^{X}+x \subset U$. By the linearity of $T$, we obtain $B_{r\varepsilon}^Y \subset T(B_{\varepsilon}^X)$ for some small $r$. Using the linearity of $T$ again, we obtain

which shows that $T(U)$ is open, therefore $T$ is an open mapping.

Remarks

One have to notice that the completeness of $X$ and $Y$ has been used more than one time. For example, the existence of $z$ depends on the fact that Cauchy sequence converges in $X$. Also, the surjectivity of $T$ cannot be omitted, can you see why?

There are some different ways to state this theorem.

  • To every $y$ with $\lVert y \rVert < \delta$, there corresponds an $x$ with $\lVert x \rVert<1$ such that $T(x)=y$.
  • Let $U$ and $V$ be the open unit balls of the Banach spaces $X$ and $Y$. To every surjective bounded linear map, there corresponds a $\delta>0$ such that

You may also realize that we have used a lot of basic definitions of topology. For example, we checked the openness of $T(U)$ by using neighborhood. The set $\overline{T(B_1^X)}$ should also remind you of limit point.

The difference of open mapping and continuous mapping can be viewed via the topologies of two topological vector spaces. Suppose $f: X \to Y$. If for any $U \in \tau_X$, we have $f(U) \in \tau_Y$, where $\tau_X$ and $\tau_Y$ are the topologies of $X$ and $Y$, respectively. But this has nothing to do with continuity. By continuity we mean, for any $V \in \tau_Y$, we have $f^{-1}(V) \in \tau_U$.

Fortunately, this theorem can be generalized to $F$-spaces, which will be demonstrated in the following blog post of the series. A space $X$ is an $F$-space if its topology $\tau$ is induced by a complete invariant metric $d$. Still, completeness plays a critical rule.

The series

Since there is no strong reason to write more posts on this topic, i.e. the three fundamental theorems of linear functional analysis, I think it’s time to make a list of the series. It’s been around half a year.

Posted Updated Analysis / Functional Analysis

The Big Three Pt. 2 - The Banach-Steinhaus Theorem

About this blog post

People call the Banach-Steinhaus theorem the first of the big three, which sits at the foundation of linear functional analysis. None of them can go without the Baire’s category theorem.

This blog post offers the Banach-Steinhaus theorem on different abstract levels. Recall that we have

First, there will be a simple version for Banach spaces, which may be more frequently used, and you will realize why it’s referred to as the uniform boundedness principle. After that, there will be a much more generalized version for TVS. Typically, the metrization of the space will not be considered.

Also, it will be a good chance to get a better view of the first and second space by Baire.

Equicontinuity

For metric spaces, equicontinuity is defined as follows. Let $(X,d_X)$ and $(Y,d_Y)$ be two metric spaces.

Let $\Lambda$ be a collection of functions from $X$ to $Y$. We have three different levels of equicontinuity.

  1. Equicontinuous at a point. For $x_0 \in X$, if for every $\varepsilon>0$, there exists a $\delta>0$ such that $d_Y(Lx_0,Lx)<\varepsilon$ for all $L \in \Lambda$ and $d_X(x_0,x)<\delta$ (that is, the continuity holds for all $L$ in a ball centered at $x_0$ with radius $r$).
  2. Pointwise equicontinuous. $\Lambda$ is equicontinuous at each point of $X$.
  3. Uniformly equicontinuous. For every $\varepsilon>0$, there exists a $\delta>0$ such that $d_Y(Lx,Ly)<\varepsilon$ for all $x \in \Lambda$ and $x,y \in X$ such that $d_X(x,y) < \delta$.

Indeed, if $\Lambda$ contains only one element, namely $L$, then everything goes with the continuity and uniform continuity.

But for Banach-Steinhaus theorem, we need a little more restrictions. In fact, $X$ and $Y$ should be considered Banach spaces, and $\Lambda$ contains linear functions only. In this sense, for $L \in \Lambda$, we have the following three conditions equivalent.

  1. $L$ is bounded.
  2. $L$ is continuous.
  3. $L$ is continuous at one point of $X$.

For topological vector spaces, where only topology and linear structure are taken into consideration, things get different. Since no metrization is considered, we have to state it in the language of topology.

Suppose $X$ and $Y$ are TVS and $\Lambda$ is a collection of linear functions from $X$ to $Y$. $\Lambda$ is equicontinuous if for every neighborhood $N$ of $0$ in $Y$, there corresponds a neighborhood $V$ of $0$ in $X$ such that $L(V) \subset N$ for all $L \in \Lambda$.

Indeed, for TVS, $L \in \Lambda$ has the three conditions equivalent as well. With that being said, equicontinuous collection has the boundedness property in a uniform manner. That’s why the Banach-Steinhaus theorem is always referred to as the uniform boundedness principle.

The Banach-Steinhaus theorem, a sufficient condition for being equicontinuous

Banach space version

Suppose $X$ is a Banach space, $Y$ is a normed linear space, and ${F}$ is a collection of bounded linear transformation of $X$ into $Y$, we have two equivalent statements:

  1. (The Resonance Theorem) If $\sup\limits_{L \in \Lambda}\left\Vert{L}\right\Vert=\infty$, then there exists some $x \in X$ such that $\sup\limits_{L \in {L}}\left\Vert{Lx}\right\Vert=\infty$. (In fact, these $x$ form a dense $G_\delta$.)

  2. (The Uniform Boundedness Principle) If $\sup\limits_{L \in {\Lambda}}\left\Vert{Lx}\right\Vert<\infty$ for all $x \in X$, then we have $ \left\Vert L \right\Vert \leq M$ for all $L \in {\Lambda}$ and some $M<\infty$.

  3. (A summary of 1 and 2) Either there exists an $M<\infty$ such that $\lVert L \rVert \leq M$ for all $L \in {L}$, or $\sup\lVert Lx \rVert = \infty$ for all $x$ belonging to some dense $G_\delta$ in $X$.

Proof

Though it would be easier if we finish the TVS version proof, it’s still a good idea to leave the formal proof without the help of TVS here. The equicontinuity of $\Lambda$ will be shown in the next section.

An elementary proof of the Resonance theorem

First, we offer an elementary proof in which the hardest part is the Cauchy sequence.

(Lemma) For any $x \in X$ and $r >0$, we have

where $B(x,r)=\{y \in X:\lVert x-y \rVert < r\}$.

(Proof of the lemma)

For $t \in X$ we have a simple relation

If we have $t \in B(0,r)$, then $x+t,x-t\in{B(x,r)}$. And the desired inequality follows by taking the supremum over $t \in B(0,r)$. (If you find trouble understanding this, take a look at the definition of $\lVert L \rVert$.)

Suppose now $\sup\limits_{L \in \Lambda}\left\Vert{L}\right\Vert=\infty$. Pick a sequence of linear transformation in $\Lambda$, say $(L_n)_{n=1}^{\infty}$, such that $\lVert L_n \rVert \geq 4^n$. Pick $x_0 \in X$, and for $n \geq 1$, we pick $x_n$ inductively.

Set $r_n=3^{-n}$. With $x_{n-1}$ being picked, $x_n \in B(x_{n-1},r_n)$ is picked in such a way that

(It’s easy to validate this inequality by reaching a contradiction.) Also, it’s easy to check that $(x_n)_{n=1}^{\infty}$ is Cauchy. Since $X$ is complete, $(x_n)$ converges to some $x \in X$. Further we have

Therefore we have

A topology-based proof

The previous proof is easy to understand but it’s not easy to see the topological properties of the set formed by such $x$. Thus we are offering a topology-based proof which enables us to get a topology view.

Put

and let

we claim that each $V_n$ is open. Indeed, we have to show that $x \mapsto \lVert Lx \rVert$ is continuous. It suffice to show that $\lVert\cdot\rVert$ defined in $Y$ is continuous. This follows immediately from triangle inequality since for $x,y \in Y$ we have

which implies

by interchanging $x$ and $y$, we get

Thus $x \mapsto \lVert Lx \rVert$ is continuous since it’s a composition of $\lVert\cdot\rVert$ and $L$. Hence $\varphi$, by the definition, is lower semicontinuous, which forces $V_n$ to be open.

If every $V_n$ is dense in $X$ (consider $\sup\lVert L \rVert=\infty$), then by BCT, $B=\bigcap_{n=1}^{\infty} V_n$ is dense in $X$. Since each $V_n$ is open, $B$ is a dense $G_\delta$. Again by the definition of $B$, we have $\varphi(x)=\infty$ for all $x \in B$.

If one of these sets, namely $V_N$, fails to be dense in $X$, then there exist an $x_0 \in X - V_N$ and an $r>0$ such that for $x \in B(0,r)$ we have $x_0+x \notin V_N$, which is equivalent to

considering the definition of $\varphi$, we also have

for all $L \in \Lambda$. Since $x=(x+x_0)-x_0$, we also have

Dividing $r$ on two sides, we got

therefore $\lVert L \rVert \leq M=\frac{2N}{r}$ as is to be shown. Again, this follows from the definition of $\lVert L \rVert$.

Topological vector space version

Suppose $X$ and $Y$ are topological vector spaces, $\Lambda$ is a collection of continuous linear mapping from $X$ into $Y$, and $B$ is the set of all $x \in X$ whose orbits

are bounded in $Y$. For this $B$, we have:

  • If $B$ is of the second category, then $\Lambda$ is equicontinuous.
A proof using properties of TVS

Pick balanced neighborhoods $W$ and $U$ of the origin in $Y$ such that $\overline{U} + \overline{U} \subset W$. The balanced neighborhood exists since every neighborhood of $0$ contains a balanced one.

Put

If $x \in B$, then $\Lambda(x)$ is bounded, which means that to $U$, there exists some $n$ such that $\Lambda(x) \subset nU$ (Be aware, no metric is introduced, this is the definition of boundedness in topological space). Therefore we have $x \in nE$. Consequently,

If no $nE$ is of the second category, then $B$ is of the first category. Therefore, there exists at least one $n$ such that $nE$ is of the second category. Since $x \mapsto nx$ is a homeomorphism of $X$ onto $X$, $E$ is of the second category as well. But $E$ is closed since each $L$ is continuous. Therefore $E$ has an interior point $x$. In this case, $x-E$ contains a neighborhood $V$ of $0$ in $X$, and

This proves that $\Lambda$ is equicontinuous.

Equicontinuity and uniform boundedness

We’ll show that $B=X$. But before that, we need another lemma, which states the connection between equicontinuity and uniform boundedness

(Lemma) Suppose $X$ and $Y$ are TVS, $\Gamma$ is an equicontinuous collection of linear mappings from $X$ to $Y$, and $E$ is a bounded subset of $X$. Then $Y$ has a bounded subset $F$ such that $T(E) \subset F$ for every $T \in \Gamma$.

(Proof of the lemma) We’ll show that, the set

is bounded. By the definition of equicontinuity, there is an neighborhood $V$ of the origin in $X$ such that $T(V) \subset W$ for all $T \in \Gamma$. Since $E$ is bounded, there exists some $t$ such that $E \subset tV$. For these $t$, by the definition of linear functions, we have

Therefore $F \subset tW$. $F$ is bounded.

Thus $\Lambda$ is uniformly bounded. Picking $E=\{x\}$ in the lemma, we also see $\Lambda(x)$ is bounded in $Y$ for every $x$. Thus $B=X$.

A special case when $X$ is a $F$-space or Banach space

$X$ is a $F$-space if its topology $\tau$ is induced by a complete invariant metric $d$. By BCT, $X$ is of the second category. If we already have $B=X$, in which case $B$ is of the second category, then by Banach-Steinhaus theorem, $\Lambda$ is equicontinuous. Formally speaking, we have:

If $\Lambda$ is a collection of continuous linear mappings from an $F$-space $X$ into a topological vector space $Y$, and if the sets

are bounded in $Y$ for every $x \in X$, then $\Lambda$ is equicontinuous.

Notice that all Banach spaces are $F$-spaces. Therefore we can restate the Uniform Boundedness Principle in Banach space with equicontinuity.

Suppose $X$ is a Banach space, $Y$ is a normed linear space, and ${F}$ is a collection of bounded linear transformation of $X$ into $Y$, we have:

  • (The Uniform Boundedness Principle) If $\sup\limits_{L \in {\Lambda}}\left\Vert{Lx}\right\Vert<\infty$ for all $x \in X$, then we have $|L| \le M$ for all $L \in {\Lambda}$ and some $M<\infty$. Further, $\Lambda$ is equicontinuous.

Application

Surprisingly enough, the Banach-Steinhaus theorem can be used to do Fourier analysis. An important example follows.

There is a periodic continuous function $f$ on $[0,1]$ such that the Fourier series

of $f$ diverges at $0$. $\hat{f}(n)$ is defined by

Notice that $f \mapsto \hat{f}$ is linear, and the divergence of the series at $0$ can be considered by

To invoke Banach-Steinhaus theorem, the family of linear functionals are defined by

It can be proved that

which goes to infinity as $N \to \infty$. The existence of such $f$ that

follows from the resonance theorem. Further, we also know that these $f$ are in a dense $G_\delta$ subset of the vector space generated by all periodic continuous functions on $[0,1]$.

The series

Since there is no strong reason to write more posts on this topic, i.e. the three fundamental theorems of linear functional analysis, I think it’s time to make a list of the series. It’s been around half a year.

References / Further readings

  1. arXiv:1005.1585v2
  2. W. Rudin, Real and Complex Analysis
  3. W. Rudin, Functional Analysiss
  4. Applications to Fourier series
Posted Updated Analysis / Functional Analysis

The Big Three Pt. 1 - Baire Category Theorem Explained

About the ‘Big Three’

There are three theorems about Banach spaces that occur frequently in the crux of functional analysis, which are called the ‘big three’:

  1. The Hahn-Banach Theorem
  2. The Banach-Steinhaus Theorem
  3. The Open Mapping Theorem

The incoming series of blog posts is intended to offer a self-read friendly explanation with richer details. Some basic analysis and topology backgrounds are required.

First and second category

The term ‘category’ is due to Baire, who developed the category theorem afterwards. Let $X$ be a topological space. A set $E \subset X$ is said to be nowhere dense if $\overline{E}$ has empty interior, i.e. $\text{int}(\overline{E})= \varnothing$.

There are some easy examples of nowhere dense sets. For example, suppose $X=\mathbb{R}$, equipped with the usual topology. Then $\mathbb{N}$ is nowhere dense in $\mathbb{R}$ while $\mathbb{Q}$ is not. It’s trivial since $\overline{\mathbb{N}}=\mathbb{N}$, which has empty interior. Meanwhile $\overline{\mathbb{Q}}=\mathbb{R}$. But $\mathbb{R}$ is open, whose interior is itself. The category is defined using nowhere dense set. In fact,

  • A set $S$ is of the first category if $S$ is a countable union of nowhere dense sets.
  • A set $T$ is of the second category if $T$ is not of the first category.

Baire category theorem (BCT)

In this blog post, we consider two cases: BCT in complete metric space and in locally compact Hausdorff space. These two cases have nontrivial intersection but they are not equal. There are some complete metric spaces that are not locally compact Hausdorff.

There are some classic topological spaces, for example $\mathbb{R}^n$, are both complete metric space and locally compact Hausdorff. If a locally compact Hausdorff space happens to be a topological vector space, then this space has finite dimension. Also, a topological vector space has to be Hausdorff.

By a Baire space we mean a topological space $X$ such that the intersection of every countable collection of dense open subsets of $X$ is also dense in $X$.

Baire category states that

(BCT 1) Every complete metric space is a Baire space.

(BCT 2) Every locally compact Hausdorff space is a Baire space.

By taking the complement of the definition, we can see that, every Baire space is not of the first category.

Suppose we have a sequence of sets $\{X_n\}$ where $X_n$ is dense in $X$ for all $n>0$, then $X_0=\cap_n X_n$ is also dense in $X$. Notice then $X_0^{c} = \cup_n X_n^c$, a nowhere dense set and a countable union of nowhere dense sets, i.e. of the first category.

Proving BCT 1 and BCT 2 via Choquet game

Let $X$ be the given complete metric space or locally Hausdorff space, and $\{X_n\}$ a countable collection of open subsets of $X$. Pick an arbitrary open subsets of $X$, namely $A_0$ (this is possible due to the topology defined on $X$). To prove that $\cap_n V_n$ is dense, we have to show that $A_0 \cap \left(\cap_n V_n\right) \neq \varnothing$. This follows the definition of denseness. Typically we have

A subset $A$ of $X$ is dense if and only if $A \cap U \neq \varnothing$ for all nonempty open subsets $U$ of $X$.

We pick a sequence of nonempty open sets $\{A_n\}$ inductively. With $A_{n-1}$ being picked, and since $V_n$ is open and dense in $X$, the intersection $V_n \cap A_{n-1}$ is nonempty and open. $A_n$ can be chosen such that

For BCT 1, $A_n$ can be chosen to be open balls with radius $< \frac{1}{n}$; for BCT 2, $A_n$ can be chosen such that the closure is compact. Define

Now, if $X$ is a locally compact Hausdorff space, then due to the compactness, $C$ is not empty, therefore we have

which shows that $A_0 \cap V_n \neq \varnothing$. BCT 2 is proved.

For BCT 1, we cannot follow this since it’s not ensured that $X$ has the Heine-Borel property, for example when $X$ is the Hilbert space (this is also a reason why BCT 1 and BCT 2 are not equivalent). The only tool remaining is Cauchy sequence. But how and where?

For any $\varepsilon > 0$, we have some $N$ such that $\frac{1}{N} < \varepsilon$. For all $m>n>N$, we have $A_m \subset A_n\subset A_N$, therefore the centers of $\{A_n\}$ form a Cauchy sequence, converging to some point of $K$, which implies that $K \neq \varnothing$. BCT 1 follows.

Applications of BCT

BCT will be used directly in the big three. It can be considered as the origin of them. But there are many other applications in different branches of mathematics. The applications shown below are in the same pattern: if it does not hold, then we have a Baire space of the first category, which is not possible.

$\mathbb{R}$ is uncountable

Suppose $\mathbb{R}$ is countable, then we have

where $x_n$ is a real number. But $\{x_n\}$ is nowhere dense, therefore $\mathbb{R}$ is of the first category. A contradiction.

Suppose that $f$ is an entire function, and that in every power series

has at least one coefficient is $0$, then $f$ is a polynomial (there exists a $N$ such that $c_n=0$ for all $n>N$).

You can find the proof here. We are using the fact that $\mathbb{C}$ is complete.

An infinite dimensional Banach space $B$ has no countable basis

Assume that $B$ has a countable basis $\{x_1,x_2,\cdots\}$ and define

It can be easily shown that $B_n$ is nowhere dense. In this sense, $B=\cup_n B_n$. A contradiction since $B$ is a complete metric space.

The series

Since there is no strong reason to write more posts on this topic, i.e. the three fundamental theorems of linear functional analysis, I think it’s time to make a list of the series. It’s been around half a year.

Posted Updated Analysis / Complex Analysis

More properties of zeros of an entire function

What’s going on again

In this post we discussed the topological properties of the zero points of an entire nonzero function, or roughly, how those points look like. The set of zero points contains no limit point, and at most countable (countable or finite). So if it’s finite, then we can find them out one by one. For example, the function $f(z)=z$ has simply one zero point. But what if it’s just countable? How fast the number grows?

Another question. Suppose we have an entire function $f$, and the zeros of $f$, namely $z_1,z_2,\cdots,z_n$, are ordered increasingly by moduli:

Is it possible to get a fine enough estimation of $|z_n|$? Interesting enough, we can get there with the help of Jensen’s formula.

Jensen’s formula

Suppose $\Omega=D(0;R)$, $f \in H(\Omega)$, $f(0) \neq 0$, $0<r<R$, and $z_1,z_2,\cdots,z_{n(r)}$ are the zeros of $f$ in $\overline{D}(0;R)$, then

There is no need to worry about the assumption $f(0) \neq 0$. Take another look at this proof. Every zero point $a$ has a unique positive number $m$ such that $f(z)=(z-a)^mg(z)$ and $g \in H(\Omega)$ but $g(a) \neq 0$. The number $m$ is called the order of the zero at $a$. Therefore if we have $f(0)=0$ we can simply consider another function, namely $\frac{f}{z^m}$ where $m$ is the order of zero at $0$.

We are not proving this identity at this point. But it can be done by considering the following function

where $m$ is found by ordering $z_j$ in such a way that $z_1,\cdots,z_m \in D(0;r)$ and $|z_{m+1}|=\cdots=|z_{n}|$. One can prove this identity by considering $|g(0)|$ as well as $\log|g(re^{i\theta})|$.

Several applications

The number of zeros of $f$ in $\overline{D}(0;r)$

For simplicity we shall assume $f(0)=1$ which has no loss of generality. Let

and $n(r)$ be the number of zeros of $f$ in $\overline{D}(0;r)$. By the maximum modulus theorem, we have

If we insert Jensen’s formula into this inequality and order $|z_n|$ by increasing moduli, we get

Which implies

So $n(r)$ is controlled by $M(2r)$. The second and third inequalities look tricky, which require more explanation.

First we should notice the fact that $z_n \in \overline{D}(0;R)$ for all $R \in \mathbb{R}$. Hence we have $\log\frac{2r}{|z_n|} \geq \log1=0$ for all $z_n \in \overline{D}(0;R)$. Hence the second inequality follows. For the third one, we simply have

So this is it, the rapidity with which $n(r)$ can grow is dominated by $M(r)$. Namely, the number of zeros of $f$ in the closed disc with radius $r$ is controlled by the maximum modulus of $f$ on a circle with bigger radius.

Examples based on different $M(r)$

Let’s begin with a simple example. Let $f(z)=1$, we have $M(r)=1$ for all $r$, but also we have $n(r)=0$, in which sense this estimation does nothing. Indeed, as long as $M(r)$ is bounded by a constant, which implies $f(z)$ is bounded, then by Liouville’s theorem, $f(z)$ is constant and this estimation is not available.

But if $M(r)$ grows properly, things become interesting. For example, if we have

where $A$ and $k$ are given positive numbers, we have a good enough estimation by

This estimation becomes interesting if we consider the logarithm of $n(r)$ and $r$, that is

If we have $f(z)=1-\exp(z^k)$ where $k$ is a positive integer, we have $n(r) \sim \frac{kr^k}{\pi}$, also

Lower bound of $|z_{n(r)}|$

We’ll see here, how to evaluate the lower bound of $|z_{n(r)}|$ using Jensen’s formula, provided that $M(r)$, or simply the upper bound of $f(z)$ is properly described. Without loss of generality we shall assume that $f(0)=1$. Also, we assume that the zero points of $f(z)$ are ordered by increasing moduli.

First we still consider

and see what will happen.

By Jensen’s, we have

This gives

By the arrangement of $\{z_n\}$, we have

Another example is when we have

where $\Im{z}$ means the imagine part of $z$.

We shall notice that in this case,

Following Jensen’s formula, we therefore have

Posted Updated Analysis / Integration Theory / Measure Theory

The Lebesgue-Radon-Nikodym theorem and how von Neumann proved it

An introduction

If one wants to learn the fundamental theorem of Calculus in the sense of Lebesgue integral, properties of measures have to be taken into account. In elementary calculus, one may consider something like

where $f$ is differentiable, say, everywhere on an interval. Now we restrict $f$ to be a differentiable and nondecreasing real function defined on $I=[a,b]$. There we got a one-to-one function defined by

For measurable sets $E\in\mathfrak{M}$, it can be seen that if $m(E)=0$, we have $m(g(E))=0$. Moreover, $g(E) \in \mathfrak{M}$, and $g$ is one-to-one. Therefore we can define a measure like

If we have a relation

(in fact, this is the Radon-Nikodym theorem we will prove later), the fundamental theorem of calculus for $f$ becomes somewhat clear since if $E=[a,x]$, we got $g(E)=[a+f(a),x+f(x)]$, thus we got

which trivially implies

the function $h$ looks like to be $g’=f’+1$.

We are not proving the fundamental theorem here. But this gives rise to a question. Is it possible to find a function such that

one may write as

or, more generally, a measure $\mu$ with respect to another measure $\lambda$? Does this $\mu$ exist with respect to $\lambda$? Does this $h$ exist? Lot of questions. Luckily the Lebesgue decomposition and Radon-Nikodym theorem make it possible.

Notations

Let $\mu$ be a positive measure on a $\sigma$-algebra $\mathfrak{M}$, let $\lambda$ be any arbitrary measure (positive or complex) defined on $\mathfrak{M}$.

We write

if $\lambda(E)=0$ for every $E\in\mathfrak{M}$ for which $\mu(E)=0$. (You may write $\mu \ll m$ in the previous section.) We say $\lambda$ is absolutely continuous with respect to $\mu$.

Another relation between measures worth consideration is being mutually singular. If we have $\lambda(E)=\lambda(A \cap E)$ for every $E \in \mathfrak{M}$, we say $\lambda$ is concentrated on $A$.

If we now have two measures $\mu_1$ and $\mu_2$, two disjoint sets $A$ and $B$ such that $\mu_1$ is concentrated on $A$, $\mu_2$ is concentrated on $B$, we say $\mu_1$ and $\mu_2$ are mutually singular, and write

The Theorem of Lebesgue-Radon-Nikodym

Let $\mu$ be a positive $\sigma$-finite measure on $\mathfrak{M}$, and $\lambda$ a complex measure on $\mathfrak{M}$.

  • There exists a unique pair of complex measures $\lambda_{ac}$ and $\lambda_{s}$ on $\mathfrak{M}$ such that
  • There is a unique $h \in L^1(\mu)$ such that

for every $E \in \mathfrak{M}$.

The unique pair $(\lambda_{ac},\lambda_s)$ is called the Lebesgue decomposition; the existence of $h$ is called the Radon-Nikodym theorem, and $h$ is called the Radon-Nikodym derivative. One also writes $d\lambda_{ac}=hd\mu$ or $\frac{d\lambda_{ac}}{d\mu}=h$ in this situation.

These are two separate theorems, but von Neumann gave the idea to prove these two at one stroke.

If we already have $\lambda \ll \mu$, then $\lambda_s=0$ and the Radon-Nikodym derivative shows up in the natural of things.

Also, one cannot ignore the fact that $m$ the Lebesgue measure is $\sigma$-finite.

Proof explained

Step 1 - Construct a bounded functional

We are going to employ Hilbert space technique in this proof. Precisely speaking, we are going to construct a bounded linear functional to find another function, namely $g$, which is the epicentre of this proof.

The boundedness of $\lambda$ is clear since it’s complex, but $\mu$ is only assumed to be $\sigma$-finite. Therefore we need some adjustment onto $\mu$.

1.1 Replacing $\mu$ with a finite measure

If $\mu$ is a positive $\sigma$-finite measure on a $\sigma$-algebra $\mathfrak{M}$ in a set $X$, then there is a function $w$ such that $w \in L^1(\mu)$ and $0<w(x)<1$ for every $x \in X$.

The $\sigma$-finiteness of $\mu$ denotes that, there exist some sets $E_n$ such that

and that $\mu(E_n)<\infty$ for all $n$.

Define

(you can also say that $w_n=\frac{1}{2^n(1+\mu(E_n))}\chi_{E_n}$), then we have

satisfies $0<w<1$ for all $x$. With $w$, we are able to define a new measure, namely

The fact that $\tilde{\mu}(E)$ is a measure can be validated by considering $\int_{E}wd\mu=\int_{X}\chi_{E}wd\mu$. It’s more important that $\tilde{\mu}(E)$ is bounded and $\tilde{\mu}(E)=0$ if and only if $\mu(E)=0$. The second one comes from the strict positivity of $w$. For the first one, notice that

1.2 A bounded linear functional associated with $\lambda$

Since $\lambda$ is complex, without loss of generality, we are able to assume that $\lambda$ is a positive bounded measure on $\mathfrak{M}$. By 1.1, we are able to obtain a positive bounded measure by

Following the construction of Lebesgue measure, we have

for all nonnegative measurable function $f$. Also, notice that $\lambda \leq \varphi$, we have

for $f \in L^2(\varphi)$ by Schwarz inequality.

Since $\varphi(X)<\infty$, we have

to be a bounded linear functional on $L^2(\varphi)$.

Step 2 - Find the associated function with respect to $\lambda$

Since $L^2(\varphi)$ is a Hilbert space, every bounded linear functional on a Hilbert space $H$ is given by an inner product with an element in $H$. That is, by the completeness of $L^2(\varphi)$, there exists a function $g$ such that

The properties of $L^2$ space shows that $g$ is determined almost everywhere with respect to $\varphi$.

For $E \in \mathfrak{M}$, we got

which implies $0 \leq g \leq 1$ for almost every $x$ with respect to $\varphi$. Therefore we are able to assume that $0 \leq g \leq 1$ without ruining the identity. The proof is in the bag once we define $A$ to be the set where $0 \leq g < 1$ and $B$ the set where $g=1$.

Step 3 - Generate $\lambda_{ac}$ and $\lambda_{s}$ and the Radon-Nikodym derivative at one stroke

We claim that $\lambda(A \cap E)$ and $\lambda(B \cap E)$ form the decomposition we are looking for, $\lambda_{ac}$ and $\lambda_s$, respectively. Namely, $\lambda_{ac}=\lambda(A \cap E)$, $\lambda_s=\lambda(B \cap E)$.

Proving $\lambda_s \perp \mu$

If we combine $\Lambda{f}=(f,g)$ and $\varphi=\lambda+\tilde{\mu}$ together, we have

Put $f=\chi_{B}$, we have

Since $w$ is strictly positive, we see that $\mu(B)=0$. Notice that $A \cap B = \varnothing$ and $A \cup B=X$. For $E \in \mathfrak{M}$, we write $E=E_A \cup E_B$, where $E_A \subset A$ and $E_B \subset B$. Therefore

Therefore $\mu$ is concentrated on $A$.

For $\lambda_s$, observe that

Hence $\lambda_s$ is concentrated on $B$. This observation shows that $\lambda_s \perp \mu$.

Proving $\lambda_{ac} \ll \mu$ by the Radon-Nikodym derivative

The relation that $\lambda_{ac} \ll \mu$ will be showed by the existence of the Radon-Nikodym derivative.

If we replace $f$ by

where $E \in \mathfrak{M}$, we have

Notice that

Define $h_n=g(1+g+g^2+\cdots+g^n)w$, we see that on $A$, $h_n$ converges monotonically to

By monotone convergence theorem, we got

for every $E\in\mathfrak{M}$.

The measurable function $h$ is the desired Radon-Nikodym derivative once we show that $h \in L^1(\mu)$. Replacing $E$ with $X$, we see that

Clearly, if $\mu(E)=0$, we have

which shows that

as desired.

Step 3 - Generalization onto complex measures

By far we have proved this theorem for positive bounded measure. For real bounded measure, we can apply the proceeding case to the positive and negative part of it. For all complex measures, we have

where $\lambda_1$ and $\lambda_2$ are real.

Step 4 - Uniqueness of the decomposition

If we have two Lebesgue decompositions of the same measure, namely $(\lambda_{ac},\lambda_s)$ and $(\lambda’_{ac},\lambda’_s)$, we shall show that

By the definition of the decomposition we got

with $\lambda_{ac}-\lambda_{ac}’ \ll \mu$ and $\lambda_{s}’-\lambda_{s}\perp\mu$. This implies that $\lambda’_{s}-\lambda_{s} \ll \mu$ as well.

Since $\lambda’_s-\lambda_s\perp\mu$, there exists a set with $\mu(A)=0$ on which $\lambda’_s-\lambda_s$ is concentrated; the absolute continuity shows that $\lambda’_s(E)-\lambda_s(E)=0$ for all $E \subset A$. Hence $\lambda_s’-\lambda_s$ is concentrated on $X-A$. Therefore we got $(\lambda’_s-\lambda_s)\perp(\lambda’_s-\lambda_s)$, which forces $\lambda’_s-\lambda_s=0$. The uniqueness is proved.

(Following the same process one can also show that $\lambda_{ac}\perp\lambda_s$.)

Follow

Links