In this post we develop a proof of the Riesz-Markov-Kakutani theorem on a locally compact Hausdorff space, which is the essential of the existence of the Lebesgue measure.

The Open Mapping Theorem

We are finally going to prove the open mapping theorem in $F$-space. In this version, only metric and completeness are required. Therefore it contains the Banach space version naturally.

(Theorem 0) Suppose we have the following conditions:

1. $X$ is a $F$-space,
2. $Y$ is a topological space,
3. $\Lambda: X \to Y$ is continuous and linear, and
4. $\Lambda(X)$ is of the second category in $Y$.

Then $\Lambda$ is an open mapping.

Proof. Let $B$ be a neighborhood of $0$ in $X$. Let $d$ be an invariant metric on $X$ that is compatible with the $F$-topology of $X$. Define a sequence of balls by

$$B_n=\{x:d(x,0) < \frac{r}{2^n}\}$$

where $r$ is picked in such a way that $B_0 \subset B$. To show that $\Lambda$ is an open mapping, we need to prove that there exists some neighborhood $W$ of $0$ in $Y$ such that

$$W \subset \Lambda(B).$$

To do this however, we need an auxiliary set. In fact, we will show that there exists some $W$ such that

$$W \subset \overline{\Lambda(B_1)} \subset \Lambda(B).$$

We need to prove the inclusions one by one.

---

The first inclusion requires BCT. Since $B_2 -B_2 \subset B_1$, and $Y$ is a topological space, we get

$$\overline{\Lambda(B_2)}-\overline{\Lambda(B_2)} \subset \overline{\Lambda(B_2)-\Lambda(B_2)} \subset \overline{\Lambda(B_1)}$$

Since

$$\Lambda(X)=\bigcup_{k=1}^{\infty}k\Lambda(B_2),$$

according to BCT, at least one $k\Lambda(B_2)$ is of the second category in $Y$. But scalar multiplication $y\mapsto ky$ is a homeomorphism of $Y$ onto $Y$, we see $k\Lambda(B_2)$ is of the second category for all $k$, especially for $k=1$. Therefore $\overline{\Lambda(B_2)}$ has nonempty interior, which implies that there exists some open neighborhood $W$ of $0$ in $Y$ such that $W \subset \overline{\Lambda(B_1)}$. By replacing the index, it’s easy to see this holds for all $n$. That is, for $n \geq 1$, there exists some neighborhood $W_n$ of $0$ in $Y$ such that $W_n \subset \overline{\Lambda(B_n)}$.

---

The second inclusion requires the completeness of $X$. Fix $y_1 \in \overline{\Lambda(B_1)}$, we will show that $y_1 \in \Lambda(B)$. Pick $y_n$ inductively. Assume $y_n$ has been chosen in $\overline{\Lambda(B_n)}$. As stated before, there exists some neighborhood $W_{n+1}$ of $0$ in $Y$ such that $W_{n+1} \subset \overline{\Lambda(B_{n+1})}$. Hence

$$(y_n-W_{n+1}) \cap \Lambda(B_n) \neq \varnothing$$

Therefore there exists some $x_n \in B_n$ such that

$$\Lambda x_n = y_n - W_{n+1}.$$

Put $y_{n+1}=y_n-\Lambda x_n$, we see $y_{n+1} \in W_{n+1} \subset \overline{\Lambda(B_{n+1})}$. Therefore we are able to pick $y_n$ naturally for all $n \geq 1$.

Since $d(x_n,0)<\frac{r}{2^n}$ for all $n \geq 0$, the sums $z_n=\sum_{k=1}^{n}x_k$ converges to some $z \in X$ since $X$ is a $F$-space. Notice we also have

$$\begin{aligned} d(z,0)& \leq d(x_1,0)+d(x_2,0)+\cdots \\ & < \frac{r}{2}+\frac{r}{4}+\cdots \\ & = r \end{aligned}$$

we have $z \in B_0 \subset B$.

By the continuity of $\Lambda$, we see $\lim_{n \to \infty}y_n = 0$. Notice we also have

$$\sum_{k=1}^{n} \Lambda x_k = \sum_{k=1}^{n}(y_k-y_{k+1})=y_1-y_{n+1} \to y_1 \quad (n \to \infty),$$

we see $y_1 = \Lambda z \in \Lambda(B)$.

The whole theorem is now proved, that is, $\Lambda$ is an open mapping. $\square$

Remarks

You may think the following relation comes from nowhere:

$$(y_n - W_{n+1}) \cap \Lambda(B_{n}) \neq \varnothing.$$

But it’s not. We need to review some set-point topology definitions. Notice that $y_n$ is a limit point of $\Lambda(B_n)$, and $y_n-W_{n+1}$ is a open neighborhood of $y_n$. If $(y_n - W_{n+1}) \cap \Lambda(B_{n})$ is empty, then $y_n$ cannot be a limit point.

The geometric series by

$$\frac{\varepsilon}{2}+\frac{\varepsilon}{4}+\cdots+\frac{\varepsilon}{2^n}+\cdots=\varepsilon$$

is widely used when sum is taken into account. It is a good idea to keep this technique in mind.

Corollaries

The formal proof will not be put down here, but they are quite easy to be done.

(Corollary 0) $\Lambda(X)=Y$.

This is an immediate consequence of the fact that $\Lambda$ is open. Since $Y$ is open, $\Lambda(X)$ is an open subspace of $Y$. But the only open subspace of $Y$ is $Y$ itself.

(Corollary 1) $Y$ is a $F$-space as well.

If you have already see the commutative diagram by quotient space (put $N=\ker\Lambda$), you know that the induced map $f$ is open and continuous. By treating topological spaces as groups, by corollary 0 and the first isomorphism theorem, we have

$$X/\ker\Lambda \simeq \Lambda(X)=Y.$$

Therefore $f$ is a isomorphism; hence one-to-one. Therefore $f$ is a homeomorphism as well. In this post we showed that $X/\ker{\Lambda}$ is a $F$-space, therefore $Y$ has to be a $F$-space as well. (We are using the fact that $\ker{\Lambda}$ is a closed set. But why closed?)

(Corollary 2) If $\Lambda$ is a continuous linear mapping of an $F$-space $X$ onto a $F$-space $Y$, then $\Lambda$ is open.

This is a direct application of BCT and open mapping theorem. Notice that $Y$ is now of the second category.

(Corollary 3) If the linear map $\Lambda$ in Corollary 2 is injective, then $\Lambda^{-1}:Y \to X$ is continuous.

This comes from corollary 2 directly since $\Lambda$ is open.

(Corollary 4) If $X$ and $Y$ are Banach spaces, and if $\Lambda: X \to Y$ is a continuous linear bijective map, then there exist positive real numbers $a$ and $b$ such that

$$a \lVert x \rVert \leq \lVert \Lambda{x} \rVert \leq b\rVert x \rVert$$

for every $x \in X$.

This comes from corollary 3 directly since both $\Lambda$ and $\Lambda^{-1}$ are bounded as they are continuous.

(Corollary 5) If $\tau_1 \subset \tau_2$ are vector topologies on a vector space $X$ and if both $(X,\tau_1)$ and $(X,\tau_2)$ are $F$-spaces, then $\tau_1 = \tau_2$.

This is obtained by applying corollary 3 to the identity mapping $\iota:(X,\tau_2) \to (X,\tau_1)$.

(Corollary 6) If $\lVert \cdot \rVert_1$ and $\lVert \cdot \rVert_2$ are two norms in a vector space $X$ such that

• $\lVert\cdot\rVert_1 \leq K\lVert\cdot\rVert_2$.
• $(X,\lVert\cdot\rVert_1)$ and $(X,\lVert\cdot\rVert_2)$ are Banach

Then $\lVert\cdot\rVert_1$ and $\lVert\cdot\rVert_2$ are equivalent.

This is merely a more restrictive version of corollary 5.

The series

Since there is no strong reason to write more posts on this topic, i.e. the three fundamental theorems of linear functional analysis, I think it’s time to make a list of the series. It’s been around half a year.

• The Big Three Pt. 1 - Baire Category Theorem Explained
• The Big Three Pt. 2 - The Banach-Steinhaus Theorem
• The Big Three Pt. 3 - The Open Mapping Theorem (Banach Space)
• The Big Three Pt. 4 - The Open Mapping Theorem (F-Space)
• The Big Three Pt. 5 - The Hahn-Banach Theorem (Dominated Extension)
• The Big Three Pt. 6 - Closed Graph Theorem with Applications

The Goal

We are going to show the completeness of $X/N$ where $X$ is a TVS and $N$ a closed subspace. Alongside, a bunch of useful analysis tricks will be demonstrated (and that’s why you may find this blog post a little tedious.). But what’s more important, the theorem proved here will be used in the future.

The main process

To make it clear, we should give a formal definition of $F$-space.

A topological space $X$ is an $F$-space if its topology $\tau$ is induced by a complete invariant metric $d$.

A metric $d$ on a vector space $X$ will be called invariant if for all $x,y,z \in X$, we have

$$d(x+z,y+z)=d(x,y).$$

By complete we mean every Cauchy sequence of $(X,d)$ converges.

Defining the quotient metric $\rho$

The metric can be inherited to the quotient space naturally (we will use this fact latter), that is

If $X$ is a $F$-space, $N$ is a closed subspace of a topological vector space $X$, then $X/N$ is still a $F$-space.

Suppose $d$ is a complete invariant metric compatible with $\tau_X$. The metric on $X/N$ is defined by

$$\boxed{\rho(\pi(x),\pi(y))=\inf_{z \in N}d(x-y,z)}$$

$\rho$ is a metric

Proof. First, if $\pi(x)=\pi(y)$, that is, $x-y \in N$, we see

$$\rho(\pi(x),\pi(y))=\inf_{z \in N}d(x-y,z)=d(x-y,x-y)=0.$$

If $\pi(x) \neq \pi(y)$ however, we shall show that $\rho(\pi(x),\pi(y))>0$. In this case, we have $x-y \notin N$. Since $N$ is closed, $N^c$ is open, and $x-y$ is an interior point of $X-N$. Therefore there exists an open ball $B_r(x-y)$ centered at $x-y$ with radius $r>0$ such that $B_r(x-y) \cap N = \varnothing$. Notice we have $d(x-y,z)>r$ since otherwise $z \in B_r(x-y)$. By putting

$$r_0=\sup\{r:B_r(x-y) \cap N = \varnothing\},$$

we see $d(x-y,z) \geq r_0$ for all $z \in N$ and indeed $r_0=\inf_{z \in N}d(x-y,z)>0$ (the verification can be done by contradiction). In general, $\inf_z d(x-y,z)=0$ if and only if $x-y \in \overline{N}$.

Next, we shall show that $\rho(\pi(x),\pi(y))=\rho(\pi(y),\pi(x))$, and it suffices to assume that $\pi(x) \neq \pi(y)$. Sgince $d$ is translate invariant, we get

$$\begin{aligned} d(x-y,z)&=d(x-y-z,0) \\ &=d(0,y-x+z) \\ &=d(-z,y-x) \\ &=d(y-x,-z). \end{aligned}$$

Therefore the $\inf$ of the left hand is equal to the one of the right hand. The identity is proved.

Finally, we need to verify the triangle inequality. Let $r,s,t \in X$. For any $\varepsilon>0$, there exist some $z_\varepsilon$ and $z_\varepsilon’$ such that

$$d(r-s,z_\varepsilon)<\rho(\pi(r),\pi(s))+\frac{\varepsilon}{2},\quad d(s-t,z'_\varepsilon)<\rho(\pi(s),\pi(t))+\frac{\varepsilon}{2}.$$

Since $d$ is invariant, we see

$$\begin{aligned} d(r-t,z_\varepsilon+z'_\varepsilon)&=d((r-s)+(s-t)-(z_\varepsilon+z'_\varepsilon),0) \\ &=d([(r-s)-z_\varepsilon]+[(s-t)-z'_\varepsilon],0) \\ &=d(r-s-z_\varepsilon,t-s+z'_\varepsilon) \\ &\leq d(r-s-z_\varepsilon,0)+d(t-s+z'_\varepsilon,0) \\ &=d(r-s,z_\varepsilon)+d(s-t,z'_\varepsilon) \end{aligned}$$

(I owe @LeechLattice for the inequality above.)

Therefore

$$\begin{aligned} d(r-t,z_\varepsilon+z'_\varepsilon)&\leq d(r-s,z_\varepsilon)+d(s-t,z'_\varepsilon) \\ &<\rho(\pi(r),\pi(s))+\rho(\pi(s),\pi(t))+\varepsilon. \end{aligned}$$

(Warning: This does not imply that $\rho(\pi(r),\pi(s))+\rho(\pi(s),\pi(t))=\inf_z d(r-t,z)$ since we don’t know whether it is the lower bound or not.)

If $\rho(\pi(r),\pi(s))+\rho(\pi(s),\pi(t))<\rho(\pi(r),\pi(t))$ however, let

$$0<\varepsilon<\rho(\pi(r),\pi(t))-(\rho(\pi(r),\pi(s))+\rho(\pi(s),\pi(t)))$$

then there exists some $z’’_\varepsilon=z_\varepsilon+z’_\varepsilon$ such that

$$d(r-t,z''_\varepsilon)<\rho(\pi(r),\pi(t))$$

which is a contradiction since $\rho(\pi(r),\pi(t)) \leq d(r-t,z)$ for all $z \in N$.

(We are using the $\varepsilon$ definition of $\inf$. See here.)

$\rho$ is translate invariant

Since $\pi$ is surjective, we see if $u \in X/N$, there exists some $a \in X$ such that $\pi(a)=u$. Therefore

$$\begin{aligned} \rho(\pi(x)+u,\pi(y)+u) &=\rho(\pi(x)+\pi(a),\pi(y)+\pi(a)) \\ &=\rho(\pi(x+a),\pi(y+a)) \\ &=\inf_{z \in N}d(x+a-y-a,z) \\ &=\rho(\pi(x),\pi(y)). \end{aligned}$$

$\rho$ is well-defined

If $\pi(x)=\pi(x’)$ and $\pi(y)=\pi(y’)$, we have to show that $\rho(\pi(x),\pi(y))=\rho(\pi(x’),\pi(y’))$. In fact,

$$\begin{aligned} \rho(\pi(x),\pi(y)) &\leq \rho(\pi(x),\pi(x'))+\rho(\pi(x'),\pi(y'))+\rho(\pi(y'),\pi(y)) \\ &=\rho(\pi(x'),\pi(y')) \end{aligned}$$

since $\rho(\pi(x),\pi(x’))=0$ as $\pi(x)=\pi(x’)$. Meanwhile

$$\begin{aligned} \rho(\pi(x'),\pi(y')) &\leq \rho(\pi(x'),\pi(x)) + \rho(\pi(x),\pi(y)) + \rho(\pi(y),\pi(y')) \\ &= \rho(\pi(x),\pi(y)). \end{aligned}$$

therefore $\rho(\pi(x),\pi(y))=\rho(\pi(x’),\pi(y’))$.

$\rho$ is compatible with $\tau_N$

By proving this, we need to show that a set $E \subset X/N$ is open with respect to $\tau_N$ if and only if $E$ is a union of open balls. But we need to show a generalized version:

If $\mathscr{B}$ is a local base for $\tau$, then the collection $\mathscr{B}_N$, which contains all sets $\pi(V)$ where $V \in \mathscr{B}$, forms a local base for $\tau_N$.

Proof. We already know that $\pi$ is continuous, linear and open. Therefore $\pi(V)$ is open for all $V \in \mathscr{B}$. For any open set around $E \subset X/N$ containing $\pi(0)$, we see $\pi^{-1}(E)$ is open, and we have

$$\pi^{-1}(E)=\bigcup_{V\in\mathscr{B}}V$$

and therefore

$$E=\bigcup_{V \in \mathscr{B}}\pi(V).$$

---

Now consider the local base $\mathscr{B}$ containing all open balls around $0 \in X$. Since

$$\pi(\{x:d(x,0)<r\})=\{u:\rho(u,\pi(0))<r\}$$

we see $\rho$ determines $\mathscr{B}_N$. But we have already proved that $\rho$ is invariant; hence $\mathscr{B}_N$ determines $\tau_N$.

If $d$ is complete, then $\rho$ is complete.

Once this is proved, we are able to claim that, if $X$ is a $F$-space, then $X/N$ is still a $F$-space, since its topology is induced by a complete invariant metric $\rho$.

Proof. Suppose $(x_n)$ is a Cauchy sequence in $X/N$, relative to $\rho$. There is a subsequence $(x_{n_k})$ with $\rho(x_{n_k},x_{n_{k+1}})<2^{-k}$. Since $\pi$ is surjective, we are able to pick some $z_k \in X$ such that $\pi(z_k) = x_{n_k}$ and such that

$$d(z_{k},z_{k+1})<2^{-k}.$$

(The existence can be verified by contradiction still.) By the inequality above, we see $(z_k)$ is Cauchy (can you see why?). Since $X$ is complete, $z_k \to z$ for some $z \in X$. By the continuity of $\pi$, we also see $x_{n_k} \to \pi(z)$ as $k \to \infty$. Therefore $(x_{n_k})$ converges. Hence $(x_n)$ converges since it has a convergent subsequence. $\rho$ is complete.

Remarks

This fact will be used to prove some corollaries in the open mapping theorem. For instance, for any continuous linear map $\Lambda:X \to Y$, we see $\ker(\Lambda)$ is closed, therefore if $X$ is a $F$-space, then $X/\ker(\Lambda)$ is a $F$-space as well. We will show in the future that $X/\ker(\Lambda)$ and $\Lambda(X)$ are homeomorphic if $\Lambda(X)$ is of the second category.

There are more properties that can be inherited by $X/N$ from $X$. For example, normability, metrizability, local convexity. In particular, if $X$ is Banach, then $X/N$ is Banach as well. To do this, it suffices to define the quotient norm by

$$\lVert \pi(x) \rVert = \inf\{\lVert x-z \rVert:z \in N\}.$$

I’m assuming the reader has some abstract algebra and functional analysis background. You may have learned this already in your linear algebra class, but we are making our way to functional analysis problems.

Motivation

The trouble with $L^p$ spaces

Fix $p$ with $1 \leq p \leq \infty$. It’s easy to see that $L^p(\mu)$ is a topological vector space. But it is not a metric space if we define

$$d(f,g)=\lVert f-g \rVert_p.$$

The reason is, if $d(f,g)=0$, we can only get $f=g$ a.e., but they are not strictly equal. With that being said, this function $d$ is actually a pseudo metric. This is unnatural. However, the relation $\sim$ by $f \sim g \mathbb{R}ightarrow d(f,g)=0$ is a equivalence relation. This inspires us to take the quotient set into consideration.

Vector spaces are groups anyway

For a vector space $V$, every subspace of $V$ is a normal subgroup. There is no reason to prevent ourselves from considering the quotient group and looking for some interesting properties. Further, a vector space is an abelian group, therefore any subspace is automatically normal.

Definition

Let $N$ be a subspace of a vector space $X$. For every $x \in X$, let $\pi(x)$ be the coset of $N$ that contains $x$, that is

$$\pi(x)=x+N.$$

Trivially, $\pi(x)=\pi(y)$ if and only if $x-y \in N$ (say, $\pi$ is well-defined since $N$ is a vector space). This is a linear function since we also have the addition and multiplication by

$$\pi(x)+\pi(y)=\pi(x+y) \quad \alpha\pi(x)=\pi(\alpha{x}).$$

These cosets are the elements of a vector space $X/N$, which reads, the quotient space of $X$ modulo $N$. The map $\pi$ is called the canonical map as we all know.

Examples

First, we shall treat $\mathbb{R}^2$ as a vector space, and the subspace $\mathbb{R}$, which is graphically represented by $x$-axis, as a subspace (we will write it as $X$). For a vector $v=(2,3)$, which is represented by $AB$, we see the coset $v+X$ has something special. Pick any $u \in X$, for example, $AE$, $AC$, or $AG$. We see $v+u$ has the same $y$ value. The reason is simple since we have $v+u=(2+x,3)$, where the $y$ value remains fixed however $u$ may vary.

With that being said, the set $v+X$, which is not a vector space, can be represented by $\overrightarrow{AD}$. This proceed can be generalized to $\mathbb{R}^n$ with $\mathbb{R}^m$ as a subspace with ease.

---

We now consider a fancy example. Consider all rational Cauchy sequences, that is

$$(a_n)=(a_1,a_2,\cdots)$$

where $a_k\in\mathbb{Q}$ for all $k$. In analysis class, we learned two facts.

1. Any Cauchy sequence is bounded.
2. If $(a_n)$ converges, then $(a_n)$ is Cauchy.

However, the reverse of 2 does not hold in $\mathbb{Q}$. For example, if we put $a_k=(1+\frac{1}{k})^k$, we should have the limit to be $e$, but $e \notin \mathbb{Q}$.

If we define the addition and multiplication term by term, namely

$$(a_n)+(b_n)=(a_1+b_1,a_2+b_2,\cdots)$$

and

$$(\alpha a_n)=(\alpha a_1,\alpha a_2,\cdots)$$

where $\alpha \in \mathbb{Q}$, we get a vector space (the verification is easy). The zero vector is defined by

$$(0)=(0,0,\cdots).$$

This vector space is denoted by $\overline{\mathbb{Q}}$. The subspace containing all sequences converges to $0$ will be denoted by $\overline{\mathbb{O}}$. Again, $(a_n)+\overline{\mathbb{O}}=(b_n)+\overline{\mathbb{O}}$ if and only if $(a_n-b_n) \in \overline{\mathbb{O}}$. Using the language of equivalence relation, we also say $(a_n)$ and $(b_n)$ are equivalent if $(a_n-b_n) \in \overline{\mathbb{O}}$. For example, the two following sequences are equivalent:

$$(1,1,1,\cdots,1,\cdots)\quad\quad (0.9,0.99,0.999,\cdots).$$

Actually, we will get $\mathbb{R} \simeq \overline{\mathbb{Q}}/\overline{\mathbb{O}}$ in the end. But to make sure that this quotient space is exactly the one we meet in our analysis class, there are a lot of verifications should be done.

We shall give more definitions for calculation. The multiplication of two Cauchy sequences is defined term by term à la the addition. For $\overline{\mathbb{Q}}/\overline{\mathbb{O}}$ we have

$$((a_n)+\overline{\mathbb{O}})+((b_n)+\overline{\mathbb{O}})=(a_n+b_n) + \overline{\mathbb{O}}$$

and

$$((a_n)+\overline{\mathbb{O}})((b_n)+\overline{\mathbb{O}})=(a_nb_n)+\overline{\mathbb{O}}.$$

As for inequality, a partial order has to be defined. We say $(a_n) > (0)$ if there exists some $N>0$ such that $a_n>0$ for all $n \geq N$. By $(a_n) > (b_n)$ we mean $(a_n-b_n)>(0)$ of course. For cosets, we say $(a_n)+\overline{\mathbb{O}}>\overline{\mathbb{O}}$ if $(x_n) > (0)$ for some $(x_n) \in (a_n)+\overline{\mathbb{O}}$. This is well defined. That is, if $(x_n)>(0)$, then $(y_n)>(0)$ for all $(y_n) \in (a_n)+\overline{\mathbb{O}}$.

With these operations being defined, it can be verified that $\overline{\mathbb{Q}}/\overline{\mathbb{O}}$ has the desired properties, for example, the least-upper-bound property. But this goes too far from the topic, we are not proving it here. If you are interested, you may visit here for more details.

---

Finally, we are trying to make $L^p$ a Banach space. Fix $p$ with $1 \leq p < \infty$. There is a seminorm defined for all Lebesgue measurable functions on $[0,1]$ by

$$p(f)=\lVert f \rVert_p=\left\{\int_{0}^{1}|f(t)|^pdt\right\}^{1/p}$$

$L^p$ is a vector space containing all functions $f$ with $p(f)<\infty$. But it’s not a normed space by $p$, since $p(f)=0$ only implies $f=0$ almost everywhere. However, the set $N$ which contains all functions that equal $0$ is also a vector space. Now consider the quotient space by

$$\tilde{p}(\pi(f))=p(f),$$

where $\pi$ is the canonical map of $L^p$ into $L^p/N$. We shall prove that $\tilde{p}$ is well-defined here. If $\pi(f)=\pi(g)$, we have $f-g \in N$, therefore

$$0=p(f-g)\geq |p(f)-p(g)|,$$

which forces $p(f)=p(g)$. Therefore in this case we also have $\tilde{p}(\pi(f))=\tilde{p}(\pi(g))$. This indeed ensures that $\tilde{p}$ is a norm, and $L^p/N$ a Banach space. There are some topological facts required to prove this, we are going to cover a few of them.

Topology of quotient space

Definition

We know if $X$ is a topological vector space with a topology $\tau$, then the addition and scalar multiplication are continuous. Suppose now $N$ is a closed subspace of $X$. Define $\tau_N$ by

$$\tau_N=\{E \subset X/N:\pi^{-1}(E)\in \tau\}.$$

We are expecting $\tau_N$ to be properly-defined. And fortunately, it is. Some interesting techniques will be used in the following section.

$\tau_N$ is a vector topology

There will be two steps to get this done.

$\tau_N$ is a topology.

It is trivial that $\varnothing$ and $X/N$ are elements of $\tau_N$. Other properties are immediate as well since we have

$$\pi^{-1}(A \cap B) = \pi^{-1}(A) \cap \pi^{-1}(B)$$

and

$$\pi^{-1}(\cup A_\alpha)=\cup\pi^{-1}( A_{\alpha}).$$

That said, if we have $A,B\in \tau_N$, then $A \cap B \in \tau_N$ since $\pi^{-1}(A \cap B)=\pi^{-1}(A) \cap \pi^{-1}(B) \in \tau$.

Similarly, if $A_\alpha \in \tau_N$ for all $\alpha$, we have $\cup A_\alpha \in \tau_N$. Also, by definition of $\tau_N$, $\pi$ is continuous.

$\tau_N$ is a vector topology.

First, we show that a point in $X/N$, which can be written as $\pi(x)$, is closed. Notice that $N$ is assumed to be closed, and

$$\pi^{-1}(\pi(x))=x+N$$

therefore has to be closed.

In fact, $F \subset X/N$ is $\tau_N$-closed if and only if $\pi^{-1}(F)$ is $\tau$-closed. To prove this, one needs to notice that $\pi^{-1}(F^c)=(\pi^{-1}(F))^{c}$.

Suppose $V$ is open, then

$$\pi^{-1}(\pi(V))=N+V$$

is open. By definition of $\tau_N$, we have $\pi(V) \in \tau_N$. Therefore $\pi$ is an open mapping.

If now $W$ is a neighbourhood of $0$ in $X/N$, there exists a neighbourhood $V$ of $0$ in $X$ such that

$$V + V \subset \pi^{-1}(W).$$

Hence $\pi(V)+\pi(V) \subset W$. Since $\pi$ is open, $\pi(V)$ is a neighbourhood of $0$ in $X/N$, this shows that the addition is continuous.

The continuity of scalar multiplication will be shown in a direct way (so can the addition, but the proof above is intended to offer some special technique). We already know, the scalar multiplication on $X$ by

$$\begin{aligned} \varphi:\Phi \times X &\to X \\ (\alpha,x) &\mapsto \alpha{x} \end{aligned}$$

is continuous, where $\Phi$ is the scalar field (usually $\mathbb{R}$ or $\mathbb{C}$. Now the scalar multiplication on $X/N$ is by

$$\begin{aligned} \psi: \Phi \times X/N &\to X/N \\ (\alpha,x+N) &\mapsto \alpha{x}+N. \end{aligned}$$

We see $\psi(\alpha,x+N)=\pi(\varphi(\alpha,x))$. But the composition of two continuous functions is continuous, therefore $\psi$ is continuous.

A commutative diagram by quotient space

We are going to talk about a classic commutative diagram that you already see in algebra class.

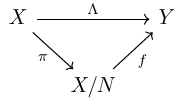
There are some assumptions.

1. $X$ and $Y$ are topological vector spaces.
2. $\Lambda$ is linear.
3. $\pi$ is the canonical map.
4. $N$ is a closed subspace of $X$ and $N \subset \ker\Lambda$.

Algebraically, there exists a unique map $f: X/N \to Y$ by $x+N \mapsto \Lambda(x)$. Namely, the diagram above is commutative. But now we are interested in some analysis facts.

$f$ is linear.

This is obvious. Since $\pi$ is surjective, for $u,v \in X/N$, we are able to find some $x,y \in X$ such that $\pi(x)=u$ and $\pi(y)=v$. Therefore we have

$$\begin{aligned} f(u+v)=f(\pi(x)+\pi(y))&=f(\pi(x+y)) \\ &=\Lambda(x+y) \\ &=\Lambda(x)+\Lambda(y) \\ &= f(\pi(x))+f(\pi(y)) \\ &=f(u)+f(v) \end{aligned}$$

and

$$\begin{aligned} f(\alpha{u})=f(\alpha\pi(x))&=f(\pi(\alpha{x})) \\ &= \Lambda(\alpha{x}) \\ &= \alpha\Lambda(x) \\ &= \alpha{f(\pi(x))} \\ &= \alpha{f(u)}. \end{aligned}$$

$\Lambda$ is open if and only if $f$ is open.

If $f$ is open, then for any open set $U \subset X$, we have

$$\Lambda(U)=f(\pi(U))$$

to be an open set since $\pi$ is open, and $\pi(U)$ is an open set.

If $f$ is not open, then there exists some $V \subset X/N$ such that $f(V)$ is closed. However, since $\pi$ is continuous, we have $\pi^{-1}(V)$ to be open. In this case, we have

$$f(\pi(\pi^{-1}(V)))=f(V)=\Lambda(\pi^{-1}(V))$$

to be closed. $\Lambda$ is therefore not open. This shows that if $\Lambda$ is open, then $f$ is open.

$\Lambda$ is continuous if and only if $f$ is continuous.

If $f$ is continuous, for any open set $W \subset Y$, we have $\pi^{-1}(f^{-1}(W))=\Lambda^{-1}(W)$ to be open. Therefore $\Lambda$ is continuous.

Conversely, if $\Lambda$ is continuous, for any open set $W \subset Y$, we have $\Lambda^{-1}(W)$ to be open. Therefore $f^{-1}(W)=\pi(\Lambda^{-1}(W))$ has to be open since $\pi$ is open.

What is open mapping

An open map is a function between two topological spaces that maps open sets to open sets. Precisely speaking, a function $f: X \to Y$ is open if for any open set $U \subset X$, $f(U)$ is open in $Y$. Likewise, a closed map is a function mapping closed sets to closed sets.

You may think open/closed map is an alternative name of continuous function. But it’s not. The definition of open/closed mapping is totally different from continuity. Here are some simple examples.

1. $f(x)=\sin{x}$ defined on $\mathbb{R}$ is not open, though it’s continuous. It can be verified by considering $(0,2\pi)$, since we have $f((0,2\pi))=[-1,1]$.
2. The projection $\pi: \mathbb{R}^2 \to \mathbb{R}$ defined by $(x,y) \mapsto x$ is open. Indeed, it maps an open ball onto an open interval on $x$ axis.
3. The inclusion map $\varphi: \mathbb{R} \to \mathbb{R}^2$ by $x \mapsto (x,0)$ however, is not open. An open interval on the plane is locally closed but not open or closed.

Under what condition will a continuous linear function between two TVS be an open mapping? We’ll give the answer in this blog post. Open mapping theorem is a sufficient condition on whether a continuous linear function is open.

Open Mapping Theorem

Let $X,Y$ be Banach spaces and $T: X \to Y$ a surjective bounded linear map. Then $T$ is an open mapping.

The open balls in $X$ and $Y$ are defined respectively by

$$B_r^X=\{x \in X:\lVert x \rVert<r\}\quad\text{and}\quad B_r^Y=\{y \in Y:\lVert y \rVert<r\}$$

All we need to do is show that there exists some $r>0$ such that

$$B_r^Y \subset T(B_1^X)$$

Since every open set in $X$ or $Y$ can be expressed as a union of open balls. For a ball in $X$ centered at $x \in X$ with radius $r$, we can express it as $x+B_r^X$. After that, it becomes obvious that $T$ maps open set to open set.

First we have

$$X=\bigcup_{n=1}^{\infty}B_n^{X}.$$

The surjectivity of $T$ ensures that

$$Y=\bigcup_{n=1}^{\infty}T(B_n^X).$$

Since $Y$ is Banach, or simply a complete metric space, by Baire category theorem, there must be some $n_0 \in \mathbb{N}$ such that $\overline{T(B_{n_0}^{X})}$ has nonempty interior. If not, which means $T(B_n^{X})$ is nowhere dense for all $n \in \mathbb{N}$, we have $Y$ is of the first category. A contradiction.

Since $x \to nx$ is a homeomorphism of $X$ onto $X$, we see in fact $T(B_n^X)$ is not nowhere dense for all $n \in \mathbb{N}$. Therefore, there exists some $y_0 \in \overline{T(B_1^{X})}$ and some $\varepsilon>0$ such that

$$y_0+B_\varepsilon^Y \subset \overline{T(B_1^X)}$$

the open set on the left hand is a neighborhood of $y_0$, which should be in the interior of $\overline{T(B_1^X)}$.

On the other hand, we claim

$$\overline{T(B_1^X)} - y_0 \subset \overline{T(B_2^X)}.$$

We shall prove it as follows. Pick any $y \in \overline{T(B_1^X)}$, we shall show that $y-y_0 \in \overline{T(B_2^X)}$. For $y_0$, there exists a sequence of $y_n$ where $\lVert y_n \rVert <1$ for all $n$ such that $Ty_n \to y_0$. Also we are able to find a sequence of $x_n$ where $\lVert x_n \rVert <1$ for all $n$ such that $Tx_n \to y$. Notice that we also have

$$y-y_0=\lim_{n \to \infty}T(x_n-y_n),$$

since

$$\lVert x_n -y_n \rVert \leq \lVert x_n \rVert+\lVert y_n \rVert <2,$$

we see $T(x_n-y_n) \in T(B_2^X)$ for all $n$, it follows that

$$y-y_0 \in \overline{T(B_2^X)}.$$

Combining all these relations, we get

$$B_\varepsilon^Y \subset \overline{T(B_2^X)}.$$

Since $T$ is linear, we see

$$2B_{\varepsilon/2}^{Y} \subset \overline{T(2B_1^X)}=2\overline{T(B_1^X)}.$$

By induction we get

$$B_{\varepsilon/2^n}^Y \subset \overline{T(B_{1/2^{n-1}}^X)}$$

for all $n \geq 1$.

We shall show however

$$B_{\varepsilon/4}^Y \subset T(B_1^X).$$

For any $u \in B_{\varepsilon/4}^Y$, we have $u \in \overline{T(B_{1/2}^X)}$. There exists some $x_1 \in B_{1/2}^{X}$ such that

$$\lVert u-Tx_1 \rVert < \frac{\varepsilon}{8}.$$

This implies that $u-Tx_1 \in B_{\varepsilon/8}^Y$. Under the same fashion, we are able to pick $x_n$ in such a way that

$$\lVert u-Tx_1-Tx_2-\cdots-Tx_n \rVert < \frac{\varepsilon}{2^{n+2}}$$

where $\lVert x_n \rVert<2^{-n}$. Now let $z_n=\sum_{k=1}^{n}x_k$, we shall show that $(z_n)$ is Cauchy. For $m<n$, we have

$$\lVert z_n - z_m \rVert =\left\Vert\sum_{k=m+1}^nx_k \right\Vert \leq \sum_{k=m+1}^{n}\lVert x_k\rVert < \frac{1}{2^{m+1}}$$

Since $X$ is Banach, there exists some $z \in X$ such that $z_n \to z$. Further we have

$$\lVert z\rVert = \lim_{n \to \infty}\lVert z_n \rVert \leq \sum_{k=1}^{\infty}\lVert x_n \rVert < 1$$

therefore $z \in B_1^X$. Since $T$ is bounded, therefore continuous, we get $T(z)=u$. To summarize, for $u \in B_{\varepsilon/4}^Y$, we have some $z \in B_{1}^X$ such that $T(z)=y$, which implies $T(B_1^X) \supset B_{\varepsilon/4}^Y$.

Let $U \subset X$ be open, we want to show that $T(U)$ is also open. Take $y \in T(U)$, then $y=T(x)$ with $x \in U$. Since $U$ is open, there exists some $\varepsilon>0$ such that $B_{\varepsilon}^{X}+x \subset U$. By the linearity of $T$, we obtain $B_{r\varepsilon}^Y \subset T(B_{\varepsilon}^X)$ for some small $r$. Using the linearity of $T$ again, we obtain

$$B_{r\varepsilon}^Y + y \subset T(B_{\varepsilon}^X+x) \subset T(U)$$

which shows that $T(U)$ is open, therefore $T$ is an open mapping.

Remarks

One have to notice that the completeness of $X$ and $Y$ has been used more than one time. For example, the existence of $z$ depends on the fact that Cauchy sequence converges in $X$. Also, the surjectivity of $T$ cannot be omitted, can you see why?

There are some different ways to state this theorem.

• To every $y$ with $\lVert y \rVert < \delta$, there corresponds an $x$ with $\lVert x \rVert<1$ such that $T(x)=y$.
• Let $U$ and $V$ be the open unit balls of the Banach spaces $X$ and $Y$. To every surjective bounded linear map, there corresponds a $\delta>0$ such that

$$T(U) \supset \delta{V}.$$

You may also realize that we have used a lot of basic definitions of topology. For example, we checked the openness of $T(U)$ by using neighborhood. The set $\overline{T(B_1^X)}$ should also remind you of limit point.

The difference of open mapping and continuous mapping can be viewed via the topologies of two topological vector spaces. Suppose $f: X \to Y$. If for any $U \in \tau_X$, we have $f(U) \in \tau_Y$, where $\tau_X$ and $\tau_Y$ are the topologies of $X$ and $Y$, respectively. But this has nothing to do with continuity. By continuity we mean, for any $V \in \tau_Y$, we have $f^{-1}(V) \in \tau_U$.

Fortunately, this theorem can be generalized to $F$-spaces, which will be demonstrated in the following blog post of the series. A space $X$ is an $F$-space if its topology $\tau$ is induced by a complete invariant metric $d$. Still, completeness plays a critical rule.

The series

Since there is no strong reason to write more posts on this topic, i.e. the three fundamental theorems of linear functional analysis, I think it’s time to make a list of the series. It’s been around half a year.

• The Big Three Pt. 1 - Baire Category Theorem Explained
• The Big Three Pt. 2 - The Banach-Steinhaus Theorem
• The Big Three Pt. 3 - The Open Mapping Theorem (Banach Space)
• The Big Three Pt. 4 - The Open Mapping Theorem (F-Space)
• The Big Three Pt. 5 - The Hahn-Banach Theorem (Dominated Extension)
• The Big Three Pt. 6 - Closed Graph Theorem with Applications

In this post we give a brief introduction too Fréchet derivatives, a generalisation of derivatives in Banach spaces, and deduce *elementary* properties.

About this blog post

People call the Banach-Steinhaus theorem the first of the big three, which sits at the foundation of linear functional analysis. None of them can go without the Baire’s category theorem.

This blog post offers the Banach-Steinhaus theorem on different abstract levels. Recall that we have

$$\text{TVS} \supset \text{Metrizable TVS} \supset \text{F-space} \supset \text{Fréchet space}\supset\text{Banach space} \supset \text{Hilbert space}$$

First, there will be a simple version for Banach spaces, which may be more frequently used, and you will realize why it’s referred to as the uniform boundedness principle. After that, there will be a much more generalized version for TVS. Typically, the metrization of the space will not be considered.

Also, it will be a good chance to get a better view of the first and second space by Baire.

Equicontinuity

For metric spaces, equicontinuity is defined as follows. Let $(X,d_X)$ and $(Y,d_Y)$ be two metric spaces.

Let $\Lambda$ be a collection of functions from $X$ to $Y$. We have three different levels of equicontinuity.

1. Equicontinuous at a point. For $x_0 \in X$, if for every $\varepsilon>0$, there exists a $\delta>0$ such that $d_Y(Lx_0,Lx)<\varepsilon$ for all $L \in \Lambda$ and $d_X(x_0,x)<\delta$ (that is, the continuity holds for all $L$ in a ball centered at $x_0$ with radius $r$).
2. Pointwise equicontinuous. $\Lambda$ is equicontinuous at each point of $X$.
3. Uniformly equicontinuous. For every $\varepsilon>0$, there exists a $\delta>0$ such that $d_Y(Lx,Ly)<\varepsilon$ for all $x \in \Lambda$ and $x,y \in X$ such that $d_X(x,y) < \delta$.

Indeed, if $\Lambda$ contains only one element, namely $L$, then everything goes with the continuity and uniform continuity.

But for Banach-Steinhaus theorem, we need a little more restrictions. In fact, $X$ and $Y$ should be considered Banach spaces, and $\Lambda$ contains linear functions only. In this sense, for $L \in \Lambda$, we have the following three conditions equivalent.

1. $L$ is bounded.
2. $L$ is continuous.
3. $L$ is continuous at one point of $X$.

---

For topological vector spaces, where only topology and linear structure are taken into consideration, things get different. Since no metrization is considered, we have to state it in the language of topology.

Suppose $X$ and $Y$ are TVS and $\Lambda$ is a collection of linear functions from $X$ to $Y$. $\Lambda$ is equicontinuous if for every neighborhood $N$ of $0$ in $Y$, there corresponds a neighborhood $V$ of $0$ in $X$ such that $L(V) \subset N$ for all $L \in \Lambda$.

Indeed, for TVS, $L \in \Lambda$ has the three conditions equivalent as well. With that being said, equicontinuous collection has the boundedness property in a uniform manner. That’s why the Banach-Steinhaus theorem is always referred to as the uniform boundedness principle.

The Banach-Steinhaus theorem, a sufficient condition for being equicontinuous

Banach space version

Suppose $X$ is a Banach space, $Y$ is a normed linear space, and ${F}$ is a collection of bounded linear transformation of $X$ into $Y$, we have two equivalent statements:

1. (The Resonance Theorem) If $\sup\limits_{L \in \Lambda}\left\Vert{L}\right\Vert=\infty$, then there exists some $x \in X$ such that $\sup\limits_{L \in {L}}\left\Vert{Lx}\right\Vert=\infty$. (In fact, these $x$ form a dense $G_\delta$.)

2. (The Uniform Boundedness Principle) If $\sup\limits_{L \in {\Lambda}}\left\Vert{Lx}\right\Vert<\infty$ for all $x \in X$, then we have $ \left\Vert L \right\Vert \leq M$ for all $L \in {\Lambda}$ and some $M<\infty$.

3. (A summary of 1 and 2) Either there exists an $M<\infty$ such that $\lVert L \rVert \leq M$ for all $L \in {L}$, or $\sup\lVert Lx \rVert = \infty$ for all $x$ belonging to some dense $G_\delta$ in $X$.

Proof

Though it would be easier if we finish the TVS version proof, it’s still a good idea to leave the formal proof without the help of TVS here. The equicontinuity of $\Lambda$ will be shown in the next section.

An elementary proof of the Resonance theorem

First, we offer an elementary proof in which the hardest part is the Cauchy sequence.

(Lemma) For any $x \in X$ and $r >0$, we have

$$\sup_{y\in B(x,r)}\lVert Lx \rVert \geq \lVert L \rVert r$$

where $B(x,r)=\{y \in X:\lVert x-y \rVert < r\}$.

(Proof of the lemma)

For $t \in X$ we have a simple relation

$$\begin{aligned} \max(\lVert{L(x+t)}\rVert,\lVert{L(x-t)}\rVert)&=\frac{1}{2}(\lVert{L(x+t)}\rVert+\lVert{L(x-t)}\rVert)+\frac{1}{2}\left\vert\lVert{L(x+t)}\rVert-\lVert{L(x-t)}\rVert\right\vert \\ &\geq \frac{1}{2}(\lVert{L(x+t)}\rVert+\lVert{L(x-t)}\rVert) \\ &\geq \frac{1}{2}\lVert{L(2t)}\rVert=\lVert Lt \rVert \end{aligned}$$

If we have $t \in B(0,r)$, then $x+t,x-t\in{B(x,r)}$. And the desired inequality follows by taking the supremum over $t \in B(0,r)$. (If you find trouble understanding this, take a look at the definition of $\lVert L \rVert$.)

Suppose now $\sup\limits_{L \in \Lambda}\left\Vert{L}\right\Vert=\infty$. Pick a sequence of linear transformation in $\Lambda$, say $(L_n)_{n=1}^{\infty}$, such that $\lVert L_n \rVert \geq 4^n$. Pick $x_0 \in X$, and for $n \geq 1$, we pick $x_n$ inductively.

Set $r_n=3^{-n}$. With $x_{n-1}$ being picked, $x_n \in B(x_{n-1},r_n)$ is picked in such a way that

$$\lVert L_n x_n \rVert \geq \frac{2}{3}\lVert L_n \rVert r_n$$

(It’s easy to validate this inequality by reaching a contradiction.) Also, it’s easy to check that $(x_n)_{n=1}^{\infty}$ is Cauchy. Since $X$ is complete, $(x_n)$ converges to some $x \in X$. Further we have

$$\begin{aligned} \lVert x-x_n \rVert &\leq \sum_{k=n}^{\infty}\lVert x_k - x_{k+1}\rVert \\ &=\frac{1}{2\cdot 3^n} \end{aligned}$$

Therefore we have

$$\begin{aligned} \lVert L_n x \rVert &=\lVert L_n[x_n-(x_n-x)] \rVert \\ &\geq \lVert L_nx_n \rVert - \lVert L_n(x_n-x) \rVert \\ &\geq \frac{2}{3}\lVert{L_n}\rVert{3}^{-n}-\lVert{L_n}\rVert\lVert{x_n-x}\rVert\\ &\geq \frac{1}{6}\lVert{L_n}\rVert{3}^{-n} \\ & \geq \frac{1}{6}\left(\frac{4}{3}\right)^n \to\infty \end{aligned}$$

A topology-based proof

The previous proof is easy to understand but it’s not easy to see the topological properties of the set formed by such $x$. Thus we are offering a topology-based proof which enables us to get a topology view.

Put

$$\varphi(x)=\sup_{L \in \Lambda}\lVert Lx \rVert$$

and let

$$V_n=\{x:\varphi(x)>n\}$$

we claim that each $V_n$ is open. Indeed, we have to show that $x \mapsto \lVert Lx \rVert$ is continuous. It suffice to show that $\lVert\cdot\rVert$ defined in $Y$ is continuous. This follows immediately from triangle inequality since for $x,y \in Y$ we have

$$\lVert x \rVert \leq \lVert x-y \rVert + \lVert y \rVert$$

which implies

$$\lVert x \rVert - \lVert y \rVert \leq \lVert x-y \rVert$$

by interchanging $x$ and $y$, we get

$$|\lVert x \rVert - \lVert y \rVert | \leq \lVert x-y \rVert$$

Thus $x \mapsto \lVert Lx \rVert$ is continuous since it’s a composition of $\lVert\cdot\rVert$ and $L$. Hence $\varphi$, by the definition, is lower semicontinuous, which forces $V_n$ to be open.

If every $V_n$ is dense in $X$ (consider $\sup\lVert L \rVert=\infty$), then by BCT, $B=\bigcap_{n=1}^{\infty} V_n$ is dense in $X$. Since each $V_n$ is open, $B$ is a dense $G_\delta$. Again by the definition of $B$, we have $\varphi(x)=\infty$ for all $x \in B$.

If one of these sets, namely $V_N$, fails to be dense in $X$, then there exist an $x_0 \in X - V_N$ and an $r>0$ such that for $x \in B(0,r)$ we have $x_0+x \notin V_N$, which is equivalent to

$$\varphi(x+x_0) \leq N$$

considering the definition of $\varphi$, we also have

$$\lVert L(x+x_0) \rVert \leq N$$

for all $L \in \Lambda$. Since $x=(x+x_0)-x_0$, we also have

$$\lVert Lx \rVert \leq \lVert L(x+x_0) \rVert+\lVert Lx_0 \rVert \leq 2N$$

Dividing $r$ on two sides, we got

$$\lVert L\frac{x}{r}\rVert \leq \frac{2N}{r}$$

therefore $\lVert L \rVert \leq M=\frac{2N}{r}$ as is to be shown. Again, this follows from the definition of $\lVert L \rVert$.

Topological vector space version

Suppose $X$ and $Y$ are topological vector spaces, $\Lambda$ is a collection of continuous linear mapping from $X$ into $Y$, and $B$ is the set of all $x \in X$ whose orbits

$$\Lambda(x)=\{Lx:L\in\Lambda\}$$

are bounded in $Y$. For this $B$, we have:

• If $B$ is of the second category, then $\Lambda$ is equicontinuous.

A proof using properties of TVS

Pick balanced neighborhoods $W$ and $U$ of the origin in $Y$ such that $\overline{U} + \overline{U} \subset W$. The balanced neighborhood exists since every neighborhood of $0$ contains a balanced one.

Put

$$E=\bigcap_{L \in \Lambda}L^{-1}(\overline{U}).$$

If $x \in B$, then $\Lambda(x)$ is bounded, which means that to $U$, there exists some $n$ such that $\Lambda(x) \subset nU$ (Be aware, no metric is introduced, this is the definition of boundedness in topological space). Therefore we have $x \in nE$. Consequently,

$$B\subset \bigcup_{n=1}^{\infty}nE.$$

If no $nE$ is of the second category, then $B$ is of the first category. Therefore, there exists at least one $n$ such that $nE$ is of the second category. Since $x \mapsto nx$ is a homeomorphism of $X$ onto $X$, $E$ is of the second category as well. But $E$ is closed since each $L$ is continuous. Therefore $E$ has an interior point $x$. In this case, $x-E$ contains a neighborhood $V$ of $0$ in $X$, and

$$L(V) \subset Lx-L(E) \subset \overline{U} - \overline{U} \subset W$$

This proves that $\Lambda$ is equicontinuous.

Equicontinuity and uniform boundedness

We’ll show that $B=X$. But before that, we need another lemma, which states the connection between equicontinuity and uniform boundedness

(Lemma) Suppose $X$ and $Y$ are TVS, $\Gamma$ is an equicontinuous collection of linear mappings from $X$ to $Y$, and $E$ is a bounded subset of $X$. Then $Y$ has a bounded subset $F$ such that $T(E) \subset F$ for every $T \in \Gamma$.

(Proof of the lemma) We’ll show that, the set

$$F=\bigcup_{T \in \Gamma}T(E)$$

is bounded. By the definition of equicontinuity, there is an neighborhood $V$ of the origin in $X$ such that $T(V) \subset W$ for all $T \in \Gamma$. Since $E$ is bounded, there exists some $t$ such that $E \subset tV$. For these $t$, by the definition of linear functions, we have

$$T(E) \subset T(tV)=tT(V) \subset tW$$

Therefore $F \subset tW$. $F$ is bounded.

Thus $\Lambda$ is uniformly bounded. Picking $E=\{x\}$ in the lemma, we also see $\Lambda(x)$ is bounded in $Y$ for every $x$. Thus $B=X$.

A special case when $X$ is a $F$-space or Banach space

$X$ is a $F$-space if its topology $\tau$ is induced by a complete invariant metric $d$. By BCT, $X$ is of the second category. If we already have $B=X$, in which case $B$ is of the second category, then by Banach-Steinhaus theorem, $\Lambda$ is equicontinuous. Formally speaking, we have:

If $\Lambda$ is a collection of continuous linear mappings from an $F$-space $X$ into a topological vector space $Y$, and if the sets

$$\Lambda(x)=\{Lx:L\in\Lambda\}$$

are bounded in $Y$ for every $x \in X$, then $\Lambda$ is equicontinuous.

Notice that all Banach spaces are $F$-spaces. Therefore we can restate the Uniform Boundedness Principle in Banach space with equicontinuity.

Suppose $X$ is a Banach space, $Y$ is a normed linear space, and ${F}$ is a collection of bounded linear transformation of $X$ into $Y$, we have:

• (The Uniform Boundedness Principle) If $\sup\limits_{L \in {\Lambda}}\left\Vert{Lx}\right\Vert<\infty$ for all $x \in X$, then we have $|L| \le M$ for all $L \in {\Lambda}$ and some $M<\infty$. Further, $\Lambda$ is equicontinuous.

Application

Surprisingly enough, the Banach-Steinhaus theorem can be used to do Fourier analysis. An important example follows.

There is a periodic continuous function $f$ on $[0,1]$ such that the Fourier series

$$\sum_{n\in\mathbb{Z}}\hat{f}(n)e^{2\pi inx}$$

of $f$ diverges at $0$. $\hat{f}(n)$ is defined by

$$\hat{f}(n)=\int_{0}^{1}e^{-2\pi inx}f(x)dx$$

Notice that $f \mapsto \hat{f}$ is linear, and the divergence of the series at $0$ can be considered by

$$\sum_{n\in\mathbb{Z}}\hat{f}(n)e^{2\pi in\cdot0}=\sum_{n\in\mathbb{Z}}\hat{f}(n)$$

To invoke Banach-Steinhaus theorem, the family of linear functionals are defined by

$$\lambda_N(f)=\sum_{|n| \leq N}\hat{f}(n)$$

It can be proved that

$$\lVert \lambda_N \rVert=\int_0^1\left\vert\sum_{|n| \leq N}e^{-2\pi inx}\right\vert dx$$

which goes to infinity as $N \to \infty$. The existence of such $f$ that

$$\sup_{N}|\lambda_N(f)|=+\infty$$

follows from the resonance theorem. Further, we also know that these $f$ are in a dense $G_\delta$ subset of the vector space generated by all periodic continuous functions on $[0,1]$.

The series

Since there is no strong reason to write more posts on this topic, i.e. the three fundamental theorems of linear functional analysis, I think it’s time to make a list of the series. It’s been around half a year.

• The Big Three Pt. 1 - Baire Category Theorem Explained
• The Big Three Pt. 2 - The Banach-Steinhaus Theorem
• The Big Three Pt. 3 - The Open Mapping Theorem (Banach Space)
• The Big Three Pt. 4 - The Open Mapping Theorem (F-Space)
• The Big Three Pt. 5 - The Hahn-Banach Theorem (Dominated Extension)
• The Big Three Pt. 6 - Closed Graph Theorem with Applications

References / Further readings

1. arXiv:1005.1585v2
2. W. Rudin, Real and Complex Analysis
3. W. Rudin, Functional Analysiss
4. Applications to Fourier series

About the ‘Big Three’

There are three theorems about Banach spaces that occur frequently in the crux of functional analysis, which are called the ‘big three’:

1. The Hahn-Banach Theorem
2. The Banach-Steinhaus Theorem
3. The Open Mapping Theorem

The incoming series of blog posts is intended to offer a self-read friendly explanation with richer details. Some basic analysis and topology backgrounds are required.

First and second category

The term ‘category’ is due to Baire, who developed the category theorem afterwards. Let $X$ be a topological space. A set $E \subset X$ is said to be nowhere dense if $\overline{E}$ has empty interior, i.e. $\text{int}(\overline{E})= \varnothing$.

There are some easy examples of nowhere dense sets. For example, suppose $X=\mathbb{R}$, equipped with the usual topology. Then $\mathbb{N}$ is nowhere dense in $\mathbb{R}$ while $\mathbb{Q}$ is not. It’s trivial since $\overline{\mathbb{N}}=\mathbb{N}$, which has empty interior. Meanwhile $\overline{\mathbb{Q}}=\mathbb{R}$. But $\mathbb{R}$ is open, whose interior is itself. The category is defined using nowhere dense set. In fact,

• A set $S$ is of the first category if $S$ is a countable union of nowhere dense sets.
• A set $T$ is of the second category if $T$ is not of the first category.

Baire category theorem (BCT)

In this blog post, we consider two cases: BCT in complete metric space and in locally compact Hausdorff space. These two cases have nontrivial intersection but they are not equal. There are some complete metric spaces that are not locally compact Hausdorff.

There are some classic topological spaces, for example $\mathbb{R}^n$, are both complete metric space and locally compact Hausdorff. If a locally compact Hausdorff space happens to be a topological vector space, then this space has finite dimension. Also, a topological vector space has to be Hausdorff.

By a Baire space we mean a topological space $X$ such that the intersection of every countable collection of dense open subsets of $X$ is also dense in $X$.

Baire category states that

(BCT 1) Every complete metric space is a Baire space.

(BCT 2) Every locally compact Hausdorff space is a Baire space.

By taking the complement of the definition, we can see that, every Baire space is not of the first category.

Suppose we have a sequence of sets $\{X_n\}$ where $X_n$ is dense in $X$ for all $n>0$, then $X_0=\cap_n X_n$ is also dense in $X$. Notice then $X_0^{c} = \cup_n X_n^c$, a nowhere dense set and a countable union of nowhere dense sets, i.e. of the first category.

Proving BCT 1 and BCT 2 via Choquet game

Let $X$ be the given complete metric space or locally Hausdorff space, and $\{X_n\}$ a countable collection of open subsets of $X$. Pick an arbitrary open subsets of $X$, namely $A_0$ (this is possible due to the topology defined on $X$). To prove that $\cap_n V_n$ is dense, we have to show that $A_0 \cap \left(\cap_n V_n\right) \neq \varnothing$. This follows the definition of denseness. Typically we have

A subset $A$ of $X$ is dense if and only if $A \cap U \neq \varnothing$ for all nonempty open subsets $U$ of $X$.

We pick a sequence of nonempty open sets $\{A_n\}$ inductively. With $A_{n-1}$ being picked, and since $V_n$ is open and dense in $X$, the intersection $V_n \cap A_{n-1}$ is nonempty and open. $A_n$ can be chosen such that

$$\overline{A}_n \subset V_n \cap A_{n-1}$$

For BCT 1, $A_n$ can be chosen to be open balls with radius $< \frac{1}{n}$; for BCT 2, $A_n$ can be chosen such that the closure is compact. Define

$$C = \bigcap_{n=1}^{\infty}\overline{A}_n$$

Now, if $X$ is a locally compact Hausdorff space, then due to the compactness, $C$ is not empty, therefore we have

$$\begin{cases} K \subset A_0 \\ K \subset V_n \quad(n \in \mathbb{N}) \end{cases}$$

which shows that $A_0 \cap V_n \neq \varnothing$. BCT 2 is proved.

For BCT 1, we cannot follow this since it’s not ensured that $X$ has the Heine-Borel property, for example when $X$ is the Hilbert space (this is also a reason why BCT 1 and BCT 2 are not equivalent). The only tool remaining is Cauchy sequence. But how and where?

For any $\varepsilon > 0$, we have some $N$ such that $\frac{1}{N} < \varepsilon$. For all $m>n>N$, we have $A_m \subset A_n\subset A_N$, therefore the centers of $\{A_n\}$ form a Cauchy sequence, converging to some point of $K$, which implies that $K \neq \varnothing$. BCT 1 follows.

Applications of BCT

BCT will be used directly in the big three. It can be considered as the origin of them. But there are many other applications in different branches of mathematics. The applications shown below are in the same pattern: if it does not hold, then we have a Baire space of the first category, which is not possible.

$\mathbb{R}$ is uncountable

Suppose $\mathbb{R}$ is countable, then we have

$$\mathbb{R}=\bigcup_{n=1}^{\infty}\{x_n\}$$

where $x_n$ is a real number. But $\{x_n\}$ is nowhere dense, therefore $\mathbb{R}$ is of the first category. A contradiction.

Suppose that $f$ is an entire function, and that in every power series

$$f(z)=\sum_{n=1}^{\infty}c_n(z-a)^n$$

has at least one coefficient is $0$, then $f$ is a polynomial (there exists a $N$ such that $c_n=0$ for all $n>N$).

You can find the proof here. We are using the fact that $\mathbb{C}$ is complete.

An infinite dimensional Banach space $B$ has no countable basis

Assume that $B$ has a countable basis $\{x_1,x_2,\cdots\}$ and define

$$B_n=\text{span}\{x_1,x_2,\cdots,x_n\}$$

It can be easily shown that $B_n$ is nowhere dense. In this sense, $B=\cup_n B_n$. A contradiction since $B$ is a complete metric space.

The series

Since there is no strong reason to write more posts on this topic, i.e. the three fundamental theorems of linear functional analysis, I think it’s time to make a list of the series. It’s been around half a year.

• The Big Three Pt. 1 - Baire Category Theorem Explained
• The Big Three Pt. 2 - The Banach-Steinhaus Theorem
• The Big Three Pt. 3 - The Open Mapping Theorem (Banach Space)
• The Big Three Pt. 4 - The Open Mapping Theorem (F-Space)
• The Big Three Pt. 5 - The Hahn-Banach Theorem (Dominated Extension)
• The Big Three Pt. 6 - Closed Graph Theorem with Applications