Projective Representations of SO(3)
Introduction
In another post we gave an exposition of irreducible representations of $SO(3)$, where we find ourselves studying harmonic polynomials on a sphere. In this post, we study another category of representations of $SO(3)$ that have its own significance in physics: projective representation. The result will be written as direct sums of irreducible representations of $SU(2)$ so the reader is advised to review the corresponding post. We recall that
Every irreducible unitary irreducible representation of $SU(2)$ is of the form $V_n$, where
Representation theory has a billion applications in physics. The group $SO(3)$ acts as the group of orientation-preserving orthogonal symmetries in $\mathbb{R}^3$ in an obvious way. The invariance under this action justifies the principle that physical reactions such as those between elementary particles should not depend on the observer’s vantage point.
Nevertheless, applications of representation theory in physics do not end at finite dimensional vector spaces. Put infinite dimensional vector spaces aside, we sometimes also need a class of vectors, in lieu of a single vector. For example, given a wavefunction $\psi$, we know $|\psi|^2$ has an interpretation of probability density. But then for any $\lambda \in S^1$, we see $|\lambda\psi|^2=|\psi|^2$, therefore $\lambda\psi$ and $\psi$ should be equivalent in a sense. By considering these equivalent classes, we find ourselves considering the projective space. Hence it makes sense to consider projective representations
where $G$ is compact. In this post we will assume $G=SO(3)$ and see how far we can go.
Simplification of Arguments
We begin with a simple group-theoretic lemma:
Lemma 1. One has
where $C_n$ is the group of $n$th roots of unity, embedded into $SL(n,\mathbb{C})$ via the map $\xi \to \xi I$.
Proof. Consider the canonical map
This map is surjective. For any $B\mathbb{C}^\ast \in GL(n,\mathbb{C})/\mathbb{C}$, we have $B\mathbb{C}^\ast=\frac{1}{|B|}B\mathbb{C}^\ast$, and $\frac{1}{|B|}B \in SL(n,\mathbb{C})$ is the preimage of $B\mathbb{C}^\ast$.
On the other hand, we see $\ker p$ consists of scalar matrices in $SL(n,\mathbb{C})$. If $\lambda I \in SL(n,\mathbb{C})$, then $|\lambda I|=\lambda^n=1$, thereby $\ker p$ can be identified as $C_n$, proving the isomorphism. $\square$
Therefore, when studying a projective representation $G \to PGL(n,\mathbb{C})$, we are quickly reduced to special linear group, which is much simpler. Besides the group of $n$th roots of unity is much simpler than the group of nonzero complex numbers.
However, our simplification has not reach the end. We will see next that special linear group can be then reduced to special unitary group. Recall that a linear matrix representation of a compact Lie group is similar to a unitary one. The following lemma is a projective analogy.
Lemma 2. Let $G$ be a compact Lie group. Every homomorphism $\varphi:G \to PGL(n,\mathbb{C})=SL(n,\mathbb{C})/C_n$ is conjugate to a homomorphism whose image lies in $SU(n)/C_n$.
Proof. Consider the fibre product $H$ of $G$ and $SL(n,\mathbb{C})$ over $PGL(n,\mathbb{C})$:
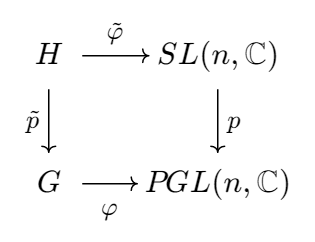
Here, $p$ is the canonical projection of $SL(n,\mathbb{C}) \to SL(n,\mathbb{C})/C_n$. It suffices to show that $\tilde\varphi$ is similar to a unitary representation. Explicitly, one has
with $\tilde\varphi:(g,A) \mapsto A$ and $\tilde{p}:(g,A) \to g$. Since $G$ is compact and $\tilde{p}$ has finite kernel $C_n$, one sees that $H$ is a compact Lie group. Therefore the matrix representation $\tilde\varphi:H \to SL(n,\mathbb{C})$ is similar to a homomorphism $H \to SU(n)$, from which the lemma follows. $\square$
Therefore we are reduced to considering homomorphisms
for sake of this post. But we are not done yet. Having to deal with a quotient group is not satisfactory anyway.
Since $SU(n)$ is simply connected (see this video), the projections $SU(n) \to SU(n)/C_n$ are universal coverings. In particular, when $n=2$, we see $SU(2) \to SU(2)/C_2 = SO(3)$ is our well-known universal covering. If we lift $\varphi$ to universal coverings, we see ourselves dealing with $SU(2) \to SU(n)$. To be precise, we have the following commutative diagram (universal cover is a functor):
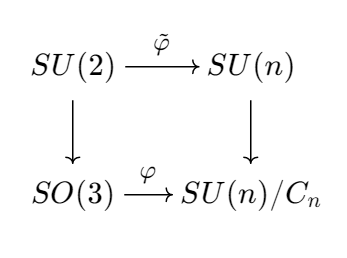
Dealing with $\tilde\varphi$ is much simpler. Physicists are more interested in unitary representations of the quaternion group $SU(2) = \operatorname{Spin}(3)$ rather than $SO(3)$, even though it looks more natural.
Discovering Projective Representations
Now we are interested in finding all unitary representations that can be pushed down to a projective representation of $SO(3)$. We have two questions:
Question 1. Does it suffice to consider maps of the form $\tilde\varphi:SU(2)\to SU(n)$?
The answer is yes. Notice that every homomorphism $f:SU(2) \to U(1)$ has to be trivial. If not, then $\ker f$ should be a nontrivial proper normal subgroup of $SU(2)$, i.e. it has to be $C_2$. But $SU(2)/C_2 \cong SO(3)$. A contradiction.
Also recall the exact sequence
Let $g:SU(2) \to U(n)$ be any homomorphism, and consider the canonical projection $\pi:U(n) \to \frac{U(n)}{SU(n)}=U(1)$. We see $\pi \circ g$ sends any elements in $SU(2)$ to $1$, meaning the image of $SU(2)$ in $U(n)$ must bee in $SU(n)$. Therefore, by considering maps of the form $SU(2) \to SU(n)$, we are not missing anything. $\square$
Question 2. What should be considered in order to determine whether $\tilde\varphi:SU(2) \to SU(n)$ can be pushed down into a morphism $\varphi:SO(3) \to SU(n)/C_n$?
The answer is, one should consider the element $-I$. Let $p:SU(2) \to SO(3)$ be the universal covering, and let $p_n:SU(n) \to SU(n)/C_n$ be the corresponding universal covering. For $\tilde\varphi:SU(2) \to SU(n)$, we want to know when there will be a homomorphism $\varphi:SO(3) \to SU(n)/C_n$ such that $p_n \circ \tilde\varphi = \varphi \circ p$.
Notice that $p(-I)=I$, therefore, should $\varphi$ exist, one has $p_n \circ \tilde\varphi(-I)=e$, the identity in the group $SU(n)/C_n$, because one should have $\varphi(I)=e$. Hence $\tilde\varphi(-I) \in \ker p_n$. Therefore $\varphi(-I)$ can be identified as a $n$th root of unity. Since $\tilde\varphi(-I)\tilde\varphi(-I)=\tilde\varphi(I)$, we see $\tilde\varphi(-I)$ should also be identified as a square root of $1$. That is, $\tilde\varphi(-I)$ is either $\operatorname{id}$ or $-\operatorname{id}$. We discuss these two cases in the following question.
On the other hand, if $\tilde\varphi(-I)=\pm\operatorname{id}$, then one can verify that $p_n \circ \tilde\varphi \circ p^{-1}$ can be well-defined. Therefore $\tilde\varphi$ can be pushed down into a morphism of $SO(3)$ if and only if $\tilde\varphi(-I)=\pm\operatorname{id}$. $\square$
Question 3. Let $W=\bigoplus_n k_n V_n$ be a representation of $SU(2)$. What will happen if it can be pushed down to a projective representation of $SO(3)$?
Let $\tilde\varphi:SU(2) \to SU(n)$ be the homomorphism corresponding to $W$. We have known for certain that when $\tilde\varphi$ can be pushed down to $SO(3)$ if and only if $\tilde\varphi(-I)=\pm\operatorname{id}$.
If $\tilde\varphi(-I)=\operatorname{id}$, then all the $n$ have to be even because the action on the polynomials cannot be the identity when $n$ is odd. If $\tilde\varphi(-I)=-\operatorname{id}$, then all the $n$ have to be odd because when $n$ is even the action of $-I$ on the polynomials must be the identity.
To be more explicit, $W=\bigoplus_n k_{2n}V_{2n}$ or $W=\bigoplus_{n}k_{2n+1}V_{2n+1}$.
Theorem 1. The projective representations of $SO(3)$ are given up to conjugations of $SU(2)$ of the form
depending on whether $(-I)$ acts by $\operatorname{id}$ or $-\operatorname{id}$.
In brief, when thinking about projective representations of $SO(3)$, one thinks about polynomials in two variables whose terms are either all even or all odd.
When studying $\tilde\varphi:SU(2) \to SU(n)$, we see $\tilde\varphi(-I)$ can be identified both as a $n$th root of unity and a square root of unity. When $n$ is odd however, we see $\tilde\varphi(-I)$ cannot be identified as $-1$, i.e. $-I$ cannot act as $-\operatorname{id}$. Unexpectedly, number theory plays a small role here.
Projective Representations of SO(3)