Chinese Remainder Theorem in Several Scenarios of Ring Theory
Every Regular Local Ring is Cohen-Macaulay
Hensel's Lemma - A Fair Application of Newton's Method and 'Double Induction'
The ring of trigonometric polynomials with complex scalars
The ring of real trigonometric polynomials
The ring
Throughout we consider the polynomial ring
This ring has a lot of non-trivial properties which give us a good chance to study commutative ring theory.
Dedekind Domain and Properties in an Elementary Approach
You can find contents about Dedekind domain (or Dedekind ring) in almost all algebraic number theory books. But many properties can be proved inside ring theory. I hope you can find the solution you need in this post, and this post will not go further than elementary ring theory. With that being said, you are assumed to have enough knowledge of ring and ring of fractions (this post serves well), but not too much mathematics maturity is assumed (at the very least you are assumed to be familiar with terminologies in the linked post).$\def\mb{\mathbb}$ $\def\mfk{\mathfrak}$
Definition
There are several ways to define Dedekind domain since there are several equivalent statements of it. We will start from the one based on ring of fractions. As a friendly reminder, $\mb{Z}$ or any principal integral domain is already a Dedekind domain. In fact Dedekind domain may be viewed as a generalization of principal integral domain.
Let $\mfk{o}$ be an integral domain (a.k.a. entire ring), and $K$ be its quotient field. A Dedekind domain is an integral domain $\mfk{o}$ such that the fractional ideals form a group under multiplication. Let’s have a breakdown. By a fractional ideal $\mfk{a}$ we mean a nontrivial additive subgroup of $K$ such that
- $\mfk{o}\mfk{a}=\mfk{a}$,
- there exists some nonzero element $c \in \mfk{o}$ such that $c\mfk{a} \subset \mfk{o}$.
What does the group look like? As you may guess, the unit element is $\mfk{o}$. For a fractional ideal $\mfk{a}$, we have the inverse to be another fractional ideal $\mfk{b}$ such that $\mfk{ab}=\mfk{ba}=\mfk{o}$. Note we regard $\mfk{o}$ as a subring of $K$. For $a \in \mfk{o}$, we treat it as $a/1 \in K$. This makes sense because the map $i:a \mapsto a/1$ is injective. For the existence of $c$, you may consider it as a restriction that the ‘denominator’ is bounded. Alternatively, we say that fractional ideal of $K$ is a finitely generated $\mfk{o}$-submodule of $K$. But in this post it is not assumed that you have learned module theory.
Let’s take $\mb{Z}$ as an example. The quotient field of $\mb{Z}$ is $\mb{Q}$. We have a fractional ideal $P$ where all elements are of the type $\frac{np}{2}$ with $p$ prime and $n \in \mb{Z}$. Then indeed we have $\mb{Z}P=P$. On the other hand, take $2 \in \mb{Z}$, we have $2P \subset \mb{Z}$. For its inverse we can take a fractional ideal $Q$ where all elements are of the type $\frac{2n}{p}$. As proved in algebraic number theory, the ring of algebraic integers in a number field is a Dedekind domain.
Before we go on we need to clarify the definition of ideal multiplication. Let $\mfk{a}$ and $\mfk{b}$ be two ideals, we define $\mfk{ab}$ to be the set of all sums
where $x_i \in \mfk{a}$ and $y_i \in \mfk{b}$. Here the number $n$ means finite but is not fixed. Alternatively we cay say $\mfk{ab}$ contains all finite sum of products of $\mfk{a}$ and $\mfk{b}$.
Propositions
(Proposition 1) A Dedekind domain $\mfk{o}$ is Noetherian.
By Noetherian ring we mean that every ideal in a ring is finitely generated. Precisely, we will prove that for every ideal $\mfk{a} \subset \mfk{o}$ there are $a_1,a_2,\cdots,a_n \in \mfk{a}$ such that, for every $r \in \mfk{a}$, we have an expression
Also note that any ideal $\mfk{a} \subset \mfk{o}$ can be viewed as a fractional ideal.
Proof. Since $\mfk{a}$ is an ideal of $\mfk{o}$, let $K$ be the quotient field of $\mfk{o}$, we see since $\mfk{oa}=\mfk{a}$, we may also view $\mfk{a}$ as a fractional ideal. Since $\mfk{o}$ is a Dedekind domain, and fractional ideals of $\mfk{a}$ is a group, there is an fractional ideal $\mfk{b}$ such that $\mfk{ab}=\mfk{ba}=\mfk{o}$. Since $1 \in \mfk{o}$, we may say that there exists some $a_1,a_2,\cdots, a_n \in \mfk{a}$ and $b_1,b_2,\cdots,b_n \in \mfk{o}$ such that $\sum_{i = 1 }^{n}a_ib_i=1$. For any $r \in \mfk{a}$, we have an expression
On the other hand, any element of the form $c_1a_1+c_2a_2+\cdots+c_na_n$, by definition, is an element of $\mfk{a}$. $\blacksquare$
From now on, the inverse of an fractional ideal $\mfk{a}$ will be written like $\mfk{a}^{-1}$.
(Proposition 2) For ideals $\mfk{a},\mfk{b} \subset \mfk{o}$, $\mfk{b}\subset\mfk{a}$ if and only if there exists some $\mfk{c}$ such that $\mfk{ac}=\mfk{b}$ (or we simply say $\mfk{a}|\mfk{b}$)
Proof. If $\mfk{b}=\mfk{ac}$, simply note that $\mfk{ac} \subset \mfk{a} \cap \mfk{c} \subset \mfk{a}$. For the converse, suppose that $a \supset \mfk{b}$, then $\mfk{c}=\mfk{a}^{-1}\mfk{b}$ is an ideal of $\mfk{o}$ since $\mfk{c}=\mfk{a}^{-1}\mfk{b} \subset \mfk{a}^{-1}\mfk{a}=\mfk{o}$, hence we may write $\mfk{b}=\mfk{a}\mfk{c}$. $\blacksquare$
(Proposition 3) If $\mfk{a}$ is an ideal of $\mfk{o}$, then there are prime ideals $\mfk{p}_1,\mfk{p}_2,\cdots,\mfk{p}_n$ such that
Proof. For this problem we use a classical technique: contradiction on maximality. Suppose this is not true, let $\mfk{A}$ be the set of ideals of $\mfk{o}$ that cannot be written as the product of prime ideals. By assumption $\mfk{U}$ is non-empty. Since as we have proved, $\mfk{o}$ is Noetherian, we can pick a maximal element $\mfk{a}$ of $\mfk{A}$ with respect to inclusion. If $\mfk{a}$ is maximal, then since all maximal ideals are prime, $\mfk{a}$ itself is prime as well. If $\mfk{a}$ is properly contained in an ideal $\mfk{m}$, then we write $\mfk{a}=\mfk{m}\mfk{m}^{-1}\mfk{a}$. We have $\mfk{m}^{-1}\mfk{a} \supsetneq \mfk{a}$ since if not, we have $\mfk{a}=\mfk{ma}$, which implies that $\mfk{m}=\mfk{o}$. But by maximality, $\mfk{m}^{-1}\mfk{a}\not\in\mfk{U}$, hence it can be written as a product of prime ideals. But $\mfk{m}$ is prime as well, we have a prime factorization for $\mfk{a}$, contradicting the definition of $\mfk{U}$.
Next we show unicity up to a permutation. If
since $\mfk{p}_1\mfk{p}_2\cdots\mfk{p}_k\subset\mfk{p}_1$ and $\mfk{p}_1$ is prime, we may assume that $\mfk{q}_1 \subset \mfk{p}_1$. By the property of fractional ideal we have $\mfk{q}_1=\mfk{p}_1\mfk{r}_1$ for some fractional ideal $\mfk{r}_1$. However we also have $\mfk{q}_1 \subset \mfk{r}_1$. Since $\mfk{q}_1$ is prime, we either have $\mfk{q}_1 \supset \mfk{p}_1$ or $\mfk{q}_1 \supset \mfk{r}_1$. In the former case we get $\mfk{p}_1=\mfk{q}_1$, and we finish the proof by continuing inductively. In the latter case we have $\mfk{r}_1=\mfk{q}_1=\mfk{p}_1\mfk{q}_1$, which shows that $\mfk{p}_1=\mfk{o}$, which is impossible. $\blacksquare$
(Proposition 4) Every nontrivial prime ideal $\mfk{p}$ is maximal.
Proof. Let $\mfk{m}$ be an maximal ideal containing $\mfk{p}$. By proposition 2 we have some $\mfk{c}$ such that $\mfk{p}=\mfk{mc}$. If $\mfk{m} \neq \mfk{p}$, then $\mfk{c} \neq \mfk{o}$, and we may write $\mfk{c}=\mfk{p}_1\cdots\mfk{p}_n$, hence $\mfk{p}=\mfk{m}\mfk{p}_1\cdots\mfk{p}_n$, which is a prime factorisation, contradicting the fact that $\mfk{p}$ has a unique prime factorisation, which is $\mfk{p}$ itself. Hence any maximal ideal containing $\mfk{p}$ is $\mfk{p}$ itself. $\blacksquare$
(Proposition 5) Suppose the Dedekind domain $\mfk{o}$ only contains one prime (and maximal) ideal $\mfk{p}$, let $t \in \mfk{p}$ and $t \not\in \mfk{p}^2$, then $\mfk{p}$ is generated by $t$.
Proof. Let $\mfk{t}$ be the ideal generated by $t$. By proposition 3 we have a factorisation
for some $n$ since $\mfk{o}$ contains only one prime ideal. According to proposition 2, if $n \geq 3$, we write $\mfk{p}^n=\mfk{p}^2\mfk{p}^{n-2}$, we see $\mfk{p}^2 \supset \mfk{p}^n$. But this is impossible since if so we have $t \in \mfk{p}^n \subset \mfk{p}^2$ contradicting our assumption. Hence $0<n<3$. But If $n=2$ we have $t \in \mfk{p}^2$ which is also not possible. So $\mfk{t}=\mfk{p}$ provided that such $t$ exists.
For the existence of $t$, note if not, then for all $t \in \mfk{p}$ we have $t \in \mfk{p}^2$, hence $\mfk{p} \subset \mfk{p}^2$. On the other hand we already have $\mfk{p}^2 = \mfk{p}\mfk{p}$, which implies that $\mfk{p}^2 \subset \mfk{p}$ (proposition 2), hence $\mfk{p}^2=\mfk{p}$, contradicting proposition 3. Hence such $t$ exists and our proof is finished. $\blacksquare$
Characterisation of Dedekind domain
In fact there is another equivalent definition of Dedekind domain:
A domain $\mfk{o}$ is Dedekind if and only if
- $\mfk{o}$ is Noetherian.
- $\mfk{o}$ is integrally closed.
- $\mfk{o}$ has Krull dimension $1$ (i.e. every non-zero prime ideals are maximal).
This is equivalent to say that faction ideals form a group and is frequently used by mathematicians as well. But we need some more advanced techniques to establish the equivalence. Presumably there will be a post about this in the future.
Tensor Product as a Universal Object (Category Theory & Module Theory)
Introduction
It is quite often to see direct sum or direct product of groups, modules, vector spaces. Indeed, for modules over a ring $R$, direct products are also direct products of $R$-modules as well. On the other hand, the direct sum is a coproduct in the category of $R$-modules.
But what about tensor products? It is some different kind of product but how? Is it related to direct product? How do we write a tensor product down? We need to solve this question but it is not a good idea to dig into numeric works.
The category of bilinear or even $n$-multilinear maps
From now on, let $R$ be a commutative ring, and $M_1,\cdots,M_n$ are $R$-modules. Mainly we work on $M_1$ and $M_2$, i.e. $M_1 \times M_2$ and $M_1 \otimes M_2$. For $n$-multilinear one, simply replace $M_1\times M_2$ with $M_1 \times M_2 \times \cdots \times M_n$ and $M_1 \otimes M_2$ with $M_1 \otimes \cdots \otimes M_n$. The only difference is the change of symbols.
The bilinear maps of $M_1 \times M_2$ determines a category, say $BL(M_1 \times M_2)$ or we simply write $BL$. For an object $(f,E)$ in this category we have $f: M_1 \times M_2 \to E$ as a bilinear map and $E$ as a $R$-module of course. For two objects $(f,E)$ and $(g,F)$, we define the morphism between them as a linear function making the following diagram commutative: $\def\mor{\operatorname{Mor}}$
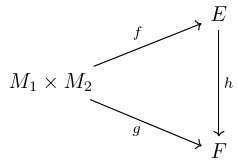
This indeed makes $BL$ a category. If we define the morphisms from $(f,E)$ to $(g,F)$ by $\mor(f,g)$ (for simplicity we omit $E$ and $F$ since they are already determined by $f$ and $g$) we see the composition
satisfy all axioms for a category:
CAT 1 Two sets $\mor(f,g)$ and $\mor(f’,g’)$ are disjoint unless $f=f’$ and $g=g’$, in which case they are equal. If $g \neq g’$ but $f = f’$ for example, for any $h \in \mor(f,g)$, we have $g = h \circ f = h \circ f’ \neq g’$, hence $h \notin \mor(f,g)$. Other cases can be verified in the same fashion.
CAT 2 The existence of identity morphism. For any $(f,E) \in BL$, we simply take the identity map $i:E \to E$. For $h \in \mor(f,g)$, we see $g = h \circ f = h \circ i \circ f$. For $h’ \in \mor(g,f)$, we see $f = h’ \circ g = i \circ h’ \circ g$.
CAT 3 The law of composition is associative when defined.
There we have a category. But what about the tensor product? It is defined to be initial (or universally repelling) object in this category. Let’s denote this object by $(\varphi,M_1 \otimes M_2)$.
For any $(f,E) \in BL$, we have a unique morphism (which is a module homomorphism as well) $h:(\varphi,M_1 \otimes M_2) \to (f,E)$. For $x \in M_1$ and $y \in M_2$, we write $\varphi(x,y)=x \otimes y$. We call the existence of $h$ the universal property of $(\varphi,M_1 \otimes M_2)$.
The tensor product is unique up to isomorphism. That is, if both $(f,E)$ and $(g,F)$ are tensor products, then $E \simeq F$ in the sense of module isomorphism. Indeed, let $h \in \mor(f,g)$ and $h’ \in \mor(g,h)$ be the unique morphisms respectively, we see $g = h \circ f$, $f = h’ \circ g$, and therefore
Hence $h \circ h’$ is the identity of $(g,F)$ and $h’ \circ h$ is the identity of $(f,E)$. This gives $E \simeq F$.
What do we get so far? For any modules that is connected to $M_1 \times M_2$ with a bilinear map, the tensor product $M_1 \oplus M_2$ of $M_1$ and $M_2$, is always able to be connected to that module with a unique module homomorphism. What if there are more than one tensor products? Never mind. All tensor products are isomorphic.
But wait, does this definition make sense? Does this product even exist? How can we study the tensor product of two modules if we cannot even write it down? So far we are only working on arrows, and we don’t know what is happening inside an module. It is not a good idea to waste our time on ‘nonsenses’. We can look into it in an natural way. Indeed, if we can find a module satisfying the property we want, then we are done, since this can represent the tensor product under any circumstances. Again, all tensor products of $M_1$ and $M_2$ are isomorphic.
A natural way to define the tensor product
Let $M$ be the free module generated by the set of all tuples $(x_1,x_2)$ where $x_1 \in M_1$ and $x_2 \in M_2$, and $N$ be the submodule generated by tuples of the following types:
First we have a inclusion map $\alpha=M_1 \times M_2 \to M$ and the canonical map $\pi:M \to M/N$. We claim that $(\pi \circ \alpha, M/N)$ is exactly what we want. But before that, we need to explain why we define such a $N$.
The reason is quite simple: We want to make sure that $\varphi=\pi \circ \alpha$ is bilinear. For example, we have $\varphi(x_1+x_1’,x_2)=\varphi(x_1,x_2)+\varphi(x_1’,x_2)$ due to our construction of $N$ (other relations follow in the same manner). This can be verified group-theoretically. Note
but
Hence we get the identity we want. For this reason we can write
Sometimes to avoid confusion people may also write $x_1 \otimes_R x_2$ if both $M_1$ and $M_2$ are $R$-modules. But before that we have to verify that this is indeed the tensor product. To verify this, all we need is the universal property of free modules.
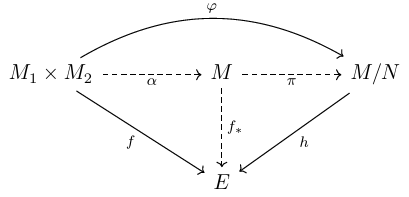
By the universal property of $M$, for any $(f,E) \in BL$, we have a induced map $f_\ast$ making the diagram inside commutative. However, for elements in $N$, we see $f_\ast$ takes value $0$, since $f_\ast$ is a bilinear map already. We finish our work by taking $h[(x,y)+N] = f_\ast(x,y)$. This is the map induced by $f_\ast$, following the property of factor module.
Trivial tensor product
For coprime integers $m,n>1$, we have $\def\mb{\mathbb}$
where $O$ means that the module only contains $0$ and $\mb{Z}/m\mb{Z}$ is considered as a module over $\mb{Z}$ for $m>1$. This suggests that, the tensor product of two modules is not necessarily ‘bigger’ than its components. Let’s see why this is trivial.
Note that for $x \in \mb{Z}/m\mb{Z}$ and $y \in \mb{Z}/n\mb{Z}$, we have
since, for example, $mx = 0$ for $x \in \mb{Z}/m\mb{Z}$ and $\varphi(0,y)=0$. If you have trouble understanding why $\varphi(0,y)=0$, just note that the submodule $N$ in our construction contains elements generated by $(0x,y)-0(x,y)$ already.
By Bézout’s identity, for any $x \otimes y$, we see there are $a$ and $b$ such that $am+bn=1$, and therefore
Hence the tensor product is trivial. This example gives us a lot of inspiration. For example, what if $m$ and $n$ are not necessarily coprime, say $\gcd(m,n)=d$? By Bézout’s identity still we have
This inspires us to study the connection between $\mb{Z}/m\mb{Z} \otimes \mb{Z}/n\mb{Z}$ and $\mb{Z}/d\mb{Z}$. By the universal property, for the bilinear map $f:\mb{Z}/m\mb{Z} \times \mb{Z}/n\mb{Z} \to \mb{Z}/d\mb{Z}$ defined by
(there should be no difficulty to verify that $f$ is well-defined), there exists a unique morphism $h:\mb{Z}/m\mb{Z} \otimes \mb{Z}/n\mb{Z} \to \mb{Z}/d\mb{Z}$ such that
Next we show that it has a natural inverse defined by
Taking $a’ = a+kd$, we show that $g(a+d\mb{Z})=g(a’+\mb{Z})$, that is, we need to show that
By Bézout’s identity, there exists some $r,s$ such that $rm+sn=d$. Hence $a’ = a + ksn+krm$, which gives
since
So $g$ is well-defined. Next we show that this is the inverse. Firstly
Secondly,
Hence $g = h^{-1}$ and we can say
If $m,n$ are coprime, then $\gcd(m,n)=1$, hence $\mb{Z}/m\mb{Z} \otimes \mb{Z}/n\mb{Z} \simeq \mb{Z}/\mb{Z}$ is trivial. More interestingly, $\mb{Z}/m\mb{Z}\otimes \mb{Z}/m\mb{Z}=\mb{Z}/m\mb{Z}$. But this elegant identity raised other questions. First of all, $\gcd(m,n)=\gcd(n,m)$, which implies
Further, for $m,n,r >1$, we have $\gcd(\gcd(m,n),r)=\gcd(m,\gcd(n,r))=\gcd(m,n,r)$, which gives
hence
Hence for modules of the form $\mb{Z}/m\mb{Z}$, we see the tensor product operation is associative and commutative up to isomorphism. Does this hold for all modules? The universal property answers this question affirmatively. From now on we will be keep using the universal property. Make sure that you have got the point already.
Tensor product as a binary operation
Let $M_1,M_2,M_3$ be $R$-modules, then there exists a unique isomorphism
for $x \in M_1$, $y \in M_2$, $z \in M_3$.
Proof. Consider the map
where $x \in M_1$. Since $(\cdot\otimes\cdot)$ is bilinear, we see $\lambda_x$ is bilinear for all $x \in M_1$. Hence by the universal property there exists a unique map of the tensor product:
Next we have the map
which is bilinear as well. Again by the universal property we have a unique map
This is indeed the isomorphism we want. The reverse is obtained by reversing the process. For the bilinear map
we get a unique map
Then from the bilinear map
we get the unique map, which is actually the reverse of $\overline{\mu}_x$:
Hence the two tensor products are isomorphic. $\square$
Let $M_1$ and $M_2$ be $R$-modules, then there exists a unique isomorphism
where $x_1 \in M_1$ and $x_2 \in M_2$.
Proof. The map
is bilinear and gives us a unique map
given by $x \otimes y \mapsto y \otimes x$. Symmetrically, the map $\lambda’:M_2 \times M_1 \to M_1 \otimes M_2$ gives us a unique map
which is the inverse of $\overline{\lambda}$. $\square$
Therefore, we may view the set of all $R$-modules as a commutative semigroup with the binary operation $\otimes$.
Maps between tensor products
Consider commutative diagram:
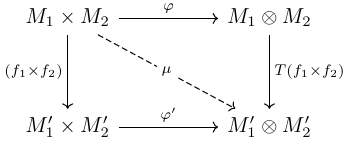
Where $f_i:M_i \to M_i’$ are some module-homomorphism. What do we want here? On the left hand, we see $f_1 \times f_2$ sends $(x_1,x_2)$ to $(f_1(x_1),f_2(x_2))$, which is quite natural. The question is, is there a natural map sending $x_1 \otimes x_2$ to $f_1(x_1) \otimes f_2(x_2)$? This is what we want from the right hand. We know $T(f_1 \times f_2)$ exists, since we have a bilinear map by $\mu = \varphi’ \circ (f_1\times f_2)$. So for $(x_1,x_2) \in M_1 \times M_2$, we have $T(f_1 \times f_2)(x_1 \otimes x_2) = \varphi’ \circ (f_1 \times f_2)(x_1,x_2) = f_1(x_1) \otimes f_2(x_2)$ as what we want.
But $T$ in this graph has more interesting properties. First of all, if $M_1 = M_1’$ an $M_2 = M_2’$, both $f_1$ and $f_2$ are identity maps, then we see $T(f_1 \times f_2)$ is the identity as well. Next, consider the following chain
We can make it a double chain:

It is obvious that $(g_1 \circ f_1 \times g_2 \circ f_2)=(g_1 \times g_2) \circ (f_1 \times f_2)$, which also gives
Hence we can say $T$ is functorial. Sometimes for simplicity we also write $T(f_1,f_2)$ or simply $f_1 \otimes f_2$, as it sends $x_1 \otimes x_2$ to $f_1(x_1) \otimes f_2(x_2)$. Indeed it can be viewed as a map
Rings of Fractions and Localisation
Is perhaps the most important technical tools in commutative algebra. In this post we are covering definitions and simple properties. Also we restrict ourselves into ring theories and no further than that. Throughout, we let $A$ be a commutative ring. With extra effort we can also make it to non-commutative rings for some results but we are not doing that here.
In fact the construction of $\mathbb{Q}$ from $\mathbb{Z}$ has already been an example. For any $a \in \mathbb{Q}$, we have some $m,n \in \mathbb{Z}$ with $n \neq 0$ such that $a = \frac{m}{n}$. As a matter of notation we may also say an ordered pair $(m,n)$ determines $a$. Two ordered pairs $(m,n)$ and $(m’,n’)$ are equivalent if and only if
But we are only using the ring structure of $\mathbb{Z}$. So it is natural to think whether it is possible to generalize this process to all rings. But we are also using the fact that $\mathbb{Z}$ is an entire ring (or alternatively integral domain, they mean the same thing). However there is a way to generalize it. $\def\mfk{\mathfrak}$
Multiplicatively closed subset
(Definition 1) A multiplicatively closed subset $S \subset A$ is a set that $1 \in S$ and if $x,y \in S$, then $xy \in S$.
For example, for $\mathbb{Z}$ we have a multiplicatively closed subset
We can also insert $0$ here but it may produce some bad result. If $S$ is also an ideal then we must have $S=A$ so this is not very interesting. However the complement is interesting.
(Proposition 1) Suppose $A$ is a commutative ring such that $1 \neq 0$. Let $S$ be a multiplicatively closed set that does not contain $0$. Let $\mfk{p}$ be the maximal element of ideals contained in $A \setminus S$, then $\mfk{p}$ is prime.
Proof. Recall that $\mfk{p}$ is prime if for any $x,y \in A$ such that $xy \in \mfk{p}$, we have $x \in \mfk{p}$ or $y \in \mfk{p}$. But now we fix $x,y \in \mfk{p}^c$. Note we have a strictly bigger ideal $\mfk{q}_1=\mfk{p}+Ax$. Since $\mfk{p}$ is maximal in the ideals contained in $A \setminus S$, we see
Therefore there exist some $a \in A$ and $p \in \mfk{p}$ such that
Also, $\mfk{q}_2=\mfk{p}+Ay$ has nontrivial intersection with $S$ (due to the maximality of $\mfk{p}$), there exist some $a’ \in A$ and $p’ \in \mfk{p}$ such that
Since $S$ is closed under multiplication, we have
But since $\mfk{p}$ is an ideal, we see $pp’+p’ax+pa’y \in \mfk{p}$. Therefore we must have $xy \notin \mfk{p}$ since if not, $(p+ax)(p’+a’y) \in \mfk{p}$, which gives $\mfk{p} \cap S \neq \varnothing$, and this is impossible. $\square$
As a corollary, for an ideal $\mfk{p} \subset A$, if $A \setminus \mfk{p}$ is multiplicatively closed, then $\mfk{p}$ is prime. Conversely, if we are given a prime ideal $\mfk{p}$, then we also get a multiplicatively closed subset.
(Proposition 2) If $\mfk{p}$ is a prime ideal of $A$, then $S = A \setminus \mfk{p}$ is multiplicatively closed.
Proof. First $1 \in S$ since $\mfk{p} \neq A$. On the other hand, if $x,y \in S$ we see $xy \in S$ since $\mfk{p}$ is prime. $\square$
Ring of fractions of a ring
We define a equivalence relation on $A \times S$ as follows:
(Proposition 3) $\sim$ is an equivalence relation.
Proof. Since $(as-as)1=0$ while $1 \in S$, we see $(a,s) \sim (a,s)$. For being symmetric, note that
Finally, to show that it is transitive, suppose $(a,s) \sim (b,t)$ and $(b,t) \sim (c,u)$. There exist $u,v \in S$ such that
This gives $bsv=atv$ and $buw = ctw$, which implies
But $tvw \in S$ since $t,v,w \in S$ and $S$ is multiplicatively closed. Hence
$\square$
Let $a/s$ denote the equivalence class of $(a,s)$. Let $S^{-1}A$ denote the set of equivalence classes (it is not a good idea to write $A/S$ as it may coincide with the notation of factor group), and we put a ring structure on $S^{-1}A$ as follows:
There is no difference between this one and the one in elementary algebra. But first of all we need to show that $S^{-1}A$ indeed form a ring.
(Proposition 4) The addition and multiplication are well defined. Further, $S^{-1}A$ is a commutative ring with identity.
Proof. Suppose $(a,s) \sim (a’,s’)$ and $(b,t) \sim (b’,t’)$ we need to show that
or
There exists $u,v \in S$ such that
If we multiply the first equation by $vtt’$ and second equation by $uss’$, we see
which is exactly what we want.
On the other hand, we need to show that
That is,
Again, we have
Hence
Since $uv \in S$, we are done.
Next we show that $S^{-1}A$ has a ring structure. If $0 \in S$, then $S^{-1}A$ contains exactly one element $0/1$ since in this case, all pairs are equivalent:
We therefore only discuss the case when $0 \notin S$. First $0/1$ is the zero element with respect to addition since
On the other hand, we have the inverse $-a/s$:
$1/1$ is the unit with respect to multiplication:
Multiplication is associative since
Multiplication is commutative since
Finally distributivity.
Note $ab/cb=a/c$ since $(abc-abc)1=0$. $\square$ $\def\mb{\mathbb}$
Cases and examples
First we consider the case when $A$ is entire. If $0 \in S$, then $S^{-1}A$ is trivial, which is not so interesting. However, provided that $0 \notin S$, we get some well-behaved result:
(Proposition 5) Let $A$ be an entire ring, and let $S$ be a multiplicatively closed subset of $A$ that does not contain $0$, then the natural map
is injective. Therefore it can be considered as a natural inclusion. Further, every element of $\varphi_S(S)$ is invertible.
Proof. Indeed, if $x/1=0/1$, then there exists $s \in S$ such that $xs=0$. Since $A$ is entire and $s \neq 0$, we see $x=0$, hence $\varphi_S$ is entire. For $s \in S$, we see $\varphi_S(s)=s/1$. However $(1/s)\varphi_S(s)=(1/s)(s/1)=s/s=1$. $\square$
Note since $A$ is entire we can also conclude that $S^{-1}A$ is entire. As a word of warning, the ring homomorphism $\varphi_S$ is not in general injective since, for example, when $0 \in S$, this map is the zero.
If we go further, making $S$ contain all non-zero element, we have:
(Proposition 6) If $A$ is entire and $S$ contains all non-zero elements of $A$, then $S^{-1}A$ is a field, called the quotient field or the field of fractions.
Proof. First we need to show that $S^{-1}A$ is entire. Suppose $(a/s)(b/t)=ab/st =0/1$ but $a/s \neq 0/1$, we see however
Since $A$ is entire, $b$ has to be $0$, which implies $b/t=0/1$. Second, if $a/s \neq 0/1$, we see $a \neq 0$ and therefore is in $S$, hence we’ve found the inverse $(a/s)^{-1}=s/a$. $\square$
In this case we can identify $A$ as a subset of $S^{-1}A$ and write $a/s=s^{-1}a$.
Let $A$ be a commutative ring, an let $S$ be the set of invertible elements of $A$. If $u \in S$, then there exists some $v \in S$ such that $uv=1$. We see $1 \in S$ and if $a,b \in S$, we have $ab \in S$ since $ab$ has an inverse as well. This set is frequently denoted by $A^\ast$, and is called the group of invertible elements of $A$. For example for $\mb{Z}$ we see $\mb{Z}^\ast$ consists of $-1$ and $1$. If $A$ is a field, then $A^\ast$ is the multiplicative group of non-zero elements of $A$. For example $\mb{Q}^\ast$ is the set of all rational numbers without $0$. For $A^\ast$ we have
If $A$ is a field, then $(A^\ast)^{-1}A \simeq A$.
Proof. Define
Then as we have already shown, $\varphi_S$ is injective. Secondly we show that $\varphi_S$ is surjective. For any $a/s \in (A^\ast)^{-1}A$, we see $as^{-1}/1 = a/s$. Therefore $\varphi_S(as^{-1})=a/s$ as is shown. $\square$
Now let’s see a concrete example. If $A$ is entire, then the polynomial ring $A[X]$ is entire. If $K = S^{-1}A$ is the quotient field of $A$, we can denote the quotient field of $A[X]$ as $K(X)$. Elements in $K(X)$ can be naturally called rational polynomials, and can be written as $f(X)/g(X)$ where $f,g \in A[X]$. For $b \in K$, we say a rational function $f/g$ is defined at $b$ if $g(b) \neq 0$. Naturally this process can be generalized to polynomials of $n$ variables.
Local ring and localization
We say a commutative ring $A$ is local if it has a unique maximal ideal. Let $\mfk{p}$ be a prime ideal of $A$, and $S = A \setminus \mfk{p}$, then $A_{\mfk{p}}=S^{-1}A$ is called the local ring of $A$ at $\mfk{p}$. Alternatively, we say the process of passing from $A$ to $A_\mfk{p}$ is localization at $\mfk{p}$. You will see it makes sense to call it localization:
(Proposition 7) $A_\mfk{p}$ is local. Precisely, the unique maximal ideal is
Note $I$ is indeed equal to $\mfk{p}A_\mfk{p}$.
Proof. First we show that $I$ is an ideal. For $b/t \in A_\mfk{p}$ and $a/s \in I$, we see
since $a \in \mfk{p}$ implies $ba \in \mfk{p}$. Next we show that $I$ is maximal, which is equivalent to show that $A_\mfk{p}/I$ is a field. For $b/t \notin I$, we have $b \in S$, hence it is legit to write $t/b$. This gives
Hence we have found the inverse.
Finally we show that $I$ is the unique maximal ideal. Let $J$ be another maximal ideal. Suppose $J \neq I$, then we can pick $m/n \in J \setminus I$. This gives $m \in S$ since if not $m \in \mfk{p}$ and then $m/n \in I$. But for $n/m \in A_\mfk{p}$ we have
This forces $J$ to be $A_\mfk{p}$ itself, contradicting the assumption that $J$ is a maximal ideal. Hence $I$ is unique. $\square$
Example
Let $p$ be a prime number, and we take $A=\mb{Z}$ and $\mfk{p}=p\mb{Z}$. We now try to determine what do $A_\mfk{p}$ and $\mfk{p}A_\mfk{p}$ look like. First $S = A \setminus \mfk{p}$ is the set of all entire numbers prime to $p$. Therefore $A_\mfk{p}$ can be considered as the ring of all rational numbers $m/n$ where $n$ is prime to $p$, and $\mfk{p}A_\mfk{p}$ can be considered as the set of all rational numbers $kp/n$ where $k \in \mb{Z}$ and $n$ is prime to $p$.
$\mb{Z}$ is the simplest example of ring and $p\mb{Z}$ is the simplest example of prime ideal. And $A_\mfk{p}$ in this case shows what does localization do: $A$ is ‘expanded’ with respect to $\mfk{p}$. Every member of $A_\mfk{p}$ is related to $\mfk{p}$, and the maximal ideal is determined by $\mfk{p}$.
Let $k$ be a infinite field. Let $A=k[x_1,\cdots,x_n]$ where $x_i$ are independent indeterminates, $\mfk{p}$ a prime ideal in $A$. Then $A_\mfk{p}$ is the ring of all rational functions $f/g$ where $g \notin \mfk{p}$. We have already defined rational functions. But we can go further and demonstrate the prototype of the local rings which arise in algebraic geometry. Let $V$ be the variety defined by $\mfk{p}$, that is,
Then what about $A_\mfk{p}$? We see since for $f/g \in A_\mfk{p}$ we have $g \notin \mfk{p}$, therefore for $g(x)$ is not equal to $0$ almost everywhere on $V$. That is, $A_\mfk{p}$ can be identified with the ring of all rational functions on $k^n$ which are defined at almost all points of $V$. We call this the local ring of $k^n$ along the variety $V$.
Universal property
Let $A$ be a ring and $S^{-1}A$ a ring of fractions, then we shall see that $\varphi_S:S \to S^{-1}A$ has a universal property.
(Proposition 8) Let $g:A \to B$ be a ring homomorphism such that $g(s)$ is invertible in $B$ for all $s \in S$, then there exists a unique homomorphism $h:S^{-1}A \to B$ such that $g = h \circ \varphi_S$.
Proof. For $a/s \in S^{-1}A$, define $h(a/s)=g(a)g(s)^{-1}$. It looks immediate but we shall show that this is what we are looking for and is unique.
Firstly we need to show that it is well defined. Suppose $a/s=a’/s’$, then there exists some $u \in S$ such that
Applying $g$ on both side yields
Since $g(x)$ is invertible for all $s \in S$, we therefore get
It is a homomorphism since
and
they are equal since
Next we show that $g=h \circ \varphi_S$. For $a \in A$, we have
Finally we show that $h$ is unique. Let $h’$ be a homomorphism satisfying the condition, then for $a \in A$ we have
For $s \in S$, we also have
Since $a/s = (a/1)(1/s)$ for all $a/s \in S^{-1}A$, we get
That is, $h’$ (or $h$) is totally determined by $g$. $\square$
Let’s restate it in the language of category theory (you can skip it if you have no idea what it is now). Let $\mfk{C}$ be the category whose objects are ring-homomorphisms
such that $f(s)$ is invertible for all $s \in S$. Then according to proposition 5, $\varphi_S$ is an object of $\mfk{C}$. For two objects $f:A \to B$ and $f’:A \to B’$, a morphism $g \in \operatorname{Mor}(f,f’)$ is a homomorphism
such that $f’=g \circ f$. So here comes the question: what is the position of $\varphi_S$?
Let $\mfk{A}$ be a category. an object $P$ of $\mfk{A}$ is called universally attracting if there exists a unique morphism of each object of $\mfk{A}$ into $P$, an is called universally repelling if for every object of $\mfk{A}$ there exists a unique morphism of $P$ into this object. Therefore we have the answer for $\mfk{C}$.
(Proposition 9) $\varphi_S$ is a universally repelling object in $\mfk{C}$.
Principal and factorial ring
An ideal $\mfk{o} \in A$ is said to be principal if there exists some $a \in A$ such that $Aa = \mfk{o}$. For example for $\mb{Z}$, the ideal
is principal and we may write $2\mb{Z}$. If every ideal of a commutative ring $A$ is principal, we say $A$ is principal. Further we say $A$ is a PID if $A$ is also an integral domain (entire). When it comes to ring of fractions, we also have the following proposition:
(Proposition 10) Let $A$ be a principal ring and $S$ a multiplicatively closed subset with $0 \notin S$, then $S^{-1}A$ is principal as well.
Proof. Let $I \subset S^{-1}A$ be an ideal. If $a \in S$ where $a/s \in I$, then we are done since then $(s/a)(a/s) = 1/1 \in I$, which implies $I=S^{-1}A$ itself, hence we shall assume $a \notin S$ for all $a/s \in I$. But for $a/s \in I$ we also have $(a/s)(s/1)=a/1 \in I$. Therefore $J=\varphi_S^{-1}(I)$ is not empty. $J$ is an ideal of $A$ since for $a \in A$ and $b \in J$, we have $\varphi_S(ab) =ab/1=(a/1)(b/1) \in I$ which implies $ab \in J$. But since $A$ is principal, there exists some $a$ such that $Aa = J$. We shall discuss the relation between $S^{-1}A(a/1)$ and $I$. For any $(c/u)(a/1)=ca/u \in S^{-1}A(a/1)$, clearly we have $ca/u \in I$, hence $S^{-1}A(a/1)\subset I$. On the other hand, for $c/u \in I$, we see $c/1=(c/u)(u/1) \in I$, hence $c \in J$, and there exists some $b \in A$ such that $c = ba$, which gives $c/u=ba/u=(b/u)(a/1) \in I$. Hence $I \subset S^{-1}A(a/1)$, and we have finally proved that $I = S^{-1}A(a/1)$. $\square$
As an immediate corollary, if $A_\mfk{p}$ is the localization of $A$ at $\mfk{p}$, and if $A$ is principal, then $A_\mfk{p}$ is principal as well. Next we go through another kind of rings. A ring is called factorial (or a unique factorization ring or UFD) if it is entire and if every non-zero element has a unique factorization into irreducible elements. An element $a \neq 0$ is called irreducible if it is not a unit and whenever $a=bc$, then either $b$ or $c$ is a unit. For all non-zero elements in a factorial ring, we have
where $u$ is a unit) (invertible).
In fact, every PID is a UFD (proof here). Irreducible elements in a factorial ring is called prime elements or simply prime (take $\mathbb{Z}$ and prime numbers as an example). Indeed, if $A$ is a factorial ring and $p$ a prime element, then $Ap$ is a prime ideal. But we are more interested in the ring of fractions of a factorial ring.
(Proposition 11) Let $A$ be a factorial ring and $S$ a multiplicatively closed subset with $0 \notin S$, then $S^{-1}A$ is factorial.
Proof. Pick $a/s \in S^{-1}A$. Since $A$ is factorial, we have $a=up_1 \cdots p_k$ where $p_i$ are primes and $u$ is a unit. But we have no idea what are irreducible elements of $S^{-1}A$. Naturally our first attack is $p_i/1$. And we have no need to restrict ourselves to $p_i$, we should work on all primes of $A$. Suppose $p$ is a prime of $A$. If $p \in S$, then $p/1 \in S$ is a unit, not prime. If $Ap \cap S \neq \varnothing$, then $rp \in S$ for some $r \in A$. But then
again $p/1$ is a unit, not prime. Finally if $Ap \cap S = \varnothing$, then $p/1$ is prime in $S^{-1}A$. For any
we see $ab=stp \not\in S$. But this also gives $ab \in Ap$ which is a prime ideal, hence we can assume $a \in Ap$ and write $a=rp$ for some $r \in A$. With this expansion we get
Hence $b/t$ is a unit, $p/1$ is a prime.
Conversely, suppose $a/s$ is irreducible in $S^{-1}A$. Since $A$ is factorial, we may write $a=u\prod_{i}p_i$. $a$ cannot be an element of $S$ since $a/s$ is not a unit. We write
We see there is some $v \in A$ such that $uv=1$ and accordingly $(u/1)(v/1)=uv/1=1/1$, hence $u/1$ is a unit. We claim that there exist a unique $p_k$ such that $1 \leq k \leq n$ and $Ap \cap S = \varnothing$. If not exists, then all $p_j/1$ are units. If both $p_{k}$ and $p_{k’}$ satisfy the requirement and $p_k \neq p_k’$, then we can write $a/s$ as
Neither the one in curly bracket nor $p_{k’}/1$ is unit, contradicting the fact that $a/s$ is irreducible. Next we show that $a/s=p_k/1$. For simplicity we write
Note $a/s = bp_k/s = (b/s)(p_k/1)$. Since $a/s$ is irreducible, $p_k/1$ is not a unit, we conclude that $b/s$ is a unit. We are done for the study of irreducible elements of $S^{-1}A$: it is of the form $p/1$ (up to a unit) where $p$ is prime in $A$ and $Ap \cap S = \varnothing$.
Now we are close to the fact that $S^{-1}A$ is also factorial. For any $a/s \in S^{-1}A$, we have an expansion
Let $p’_1,p’_2,\cdots,p’_j$ be those whose generated prime ideal has nontrivial intersection with $S$, then $p’_1/1, p’_2/1,\cdots,p’_j/1$ are units of $S^{-1}A$. Let $q_1,q_2,\cdots,q_k$ be other $p_i$’s, then $q_1/1,q_2/1,\cdots,q_k/1$ are irreducible in $S^{-1}A$. This gives
Hence $S^{-1}A$ is factorial as well. $\square$
We finish the whole post by a comprehensive proposition:
(Proposition 12) Let $A$ be a factorial ring and $p$ a prime element, $\mfk{p}=Ap$. The localization of $A$ at $\mfk{p}$ is principal.
Proof. For $a/s \in S^{-1}A$, we see $p$ does not divide $s$ since if $s = rp$ for some $r \in A$, then $s \in \mfk{p}$, contradicting the fact that $S = A \setminus \mfk{p}$. Since $A$ is factorial, we may write $a = cp^n$ for some $n \geq 0$ and $p$ does not divide $c$ as well (which gives $c \in S$. Hence $a/s = (c/s)(p^n/1)$. Note $(c/s)(s/c)=1/1$ and therefore $c/s$ is a unit. For every $a/s \in S^{-1}A$ we may write it as
where $u$ is a unit of $S^{-1}A$.
Let $I$ be any ideal in $S^{-1}A$, and
Let’s discuss the relation between $S^{-1}A(p^m/1)$ and $I$. First we see $S^{-1}A(p^m/1)=S^{-1}A(up^m/1)$ since if $v$ is the inverse of $u$, we get
Any element of $S^{-1}A(up^m/1)$ is of the form
Since $up^m/1 \in I$, we see $vup^{m+k}/1 \in I$ as well, hence $S^{-1}A(up^m/1) \subset I$. On the other hand, any element of $I$ is of the form $wup^{m+n}/1=w(p^n/1)u(p^m/1)$ where $w$ is a unit and $n \geq 0$. This shows that $vup^{m+n}/1 \in S^{-1}A(up^m/1)$. Hence $S^{-1}A(p^m/1)=S^{-1}A(up^m/1)=I$ as we wanted. $\square$